Overview
This post documents reproducible code accompanying the manuscript draft “Digital Biomarkers of Mood Disorders and Symptom Change” by Nicholas C. Jacobson, Hilary M. Weingardenm and Sabine Wilhelm (published in Nature Partner Journal (npj): Digital Medicine). This code uses machine learning to predict the diagnostic status and depressive symptom change in a a group of 23 patients with bipolar disorder or major depressive disorder and 32 non-disordered controls using actigraphy data.
The data in the following code is available publicly using the following link
Read in the data.
setwd("C:/Users/njaco/Dropbox/Depresion and Motor Activity/data")
scores=read.csv("scores.csv")Load the required packages.
library(psych) #for the rmssd function
library(e1071) #For distribution
library(mgcv) #To run stage 1 of DTVEM (see Jacobson, Chow, and Newman, 2018)## Loading required package: nlme## This is mgcv 1.8-23. For overview type 'help("mgcv-package")'.library(gtools) #For the mixsort##
## Attaching package: 'gtools'## The following object is masked from 'package:mgcv':
##
## scat## The following object is masked from 'package:e1071':
##
## permutations## The following object is masked from 'package:psych':
##
## logitlibrary(caret) #To run the machine learning techniques.## Loading required package: lattice## Loading required package: ggplot2##
## Attaching package: 'ggplot2'## The following objects are masked from 'package:psych':
##
## %+%, alphalibrary(ggplot2) #For plots
library(scales) #For plots##
## Attaching package: 'scales'## The following objects are masked from 'package:psych':
##
## alpha, rescalelibrary(Hmisc) #For correlations## Loading required package: survival##
## Attaching package: 'survival'## The following object is masked from 'package:caret':
##
## cluster## Loading required package: Formula##
## Attaching package: 'Hmisc'## The following object is masked from 'package:e1071':
##
## impute## The following object is masked from 'package:psych':
##
## describe## The following objects are masked from 'package:base':
##
## format.pval, round.POSIXt, trunc.POSIXt, unitsCreate and define biomarker new feature functions.
getmode <- function(v) {
uniqv <- unique(v)
uniqv[which.max(tabulate(match(v, uniqv)))]
}
meanvariabilitystats=function(x){
rmssd1=rmssd(x,lag=1)
rmssd2=rmssd(x,lag=2)
max1=max(x,na.rm=TRUE)
min1=min(x,na.rm=TRUE)
mean1=mean(x,na.rm=TRUE)
median1=median(x,na.rm=TRUE)
mode1=getmode(x)
sd1=sd(x,na.rm=TRUE)
skewness1=skewness(x,na.rm=TRUE)
kurtosis1=kurtosis(x,na.rm=TRUE)
quantiles1=quantile(x,seq(.01,.99,by=.01))
return(c(rmssd1,rmssd2,max1,min1,mean1,median1,mode1,sd1,skewness1,kurtosis1,quantiles1))
}
dtvemstage1=function(x){
x2=data.frame(outcome=NA,lag=NA,pred=NA)
for(i in 1:100){
outcome=x[1:(length(x)-i)]
pred=x[-1:-i]
tempx=data.frame(outcome=outcome,lag=i,pred=pred)
x2=rbind(x2,tempx)
}
out=bam(outcome~s(lag,by=pred),data=x2)
pdat=data.frame(pred=1,lag=1:100)
stage1est=predict(out,pdat,type="terms")
return(stage1est)
}Next we’ll use the functions to create a set of digital biomarkers from the actigraphy data.
setwd("C:/Users/njaco/Dropbox/Depresion and Motor Activity/data")
condlist=list.files("condition/")
condlist=mixedsort(condlist) #PUTS THEM IN NUMERICAL ORDER
conddatalist=list()
condspectrumlist=list()
condmeanvariabilitystats=list()
conddtvemstage1=list()
for(i in 1:length(condlist)){
conddatalist[[i]]=read.csv(paste("condition/",condlist[i],sep=""))
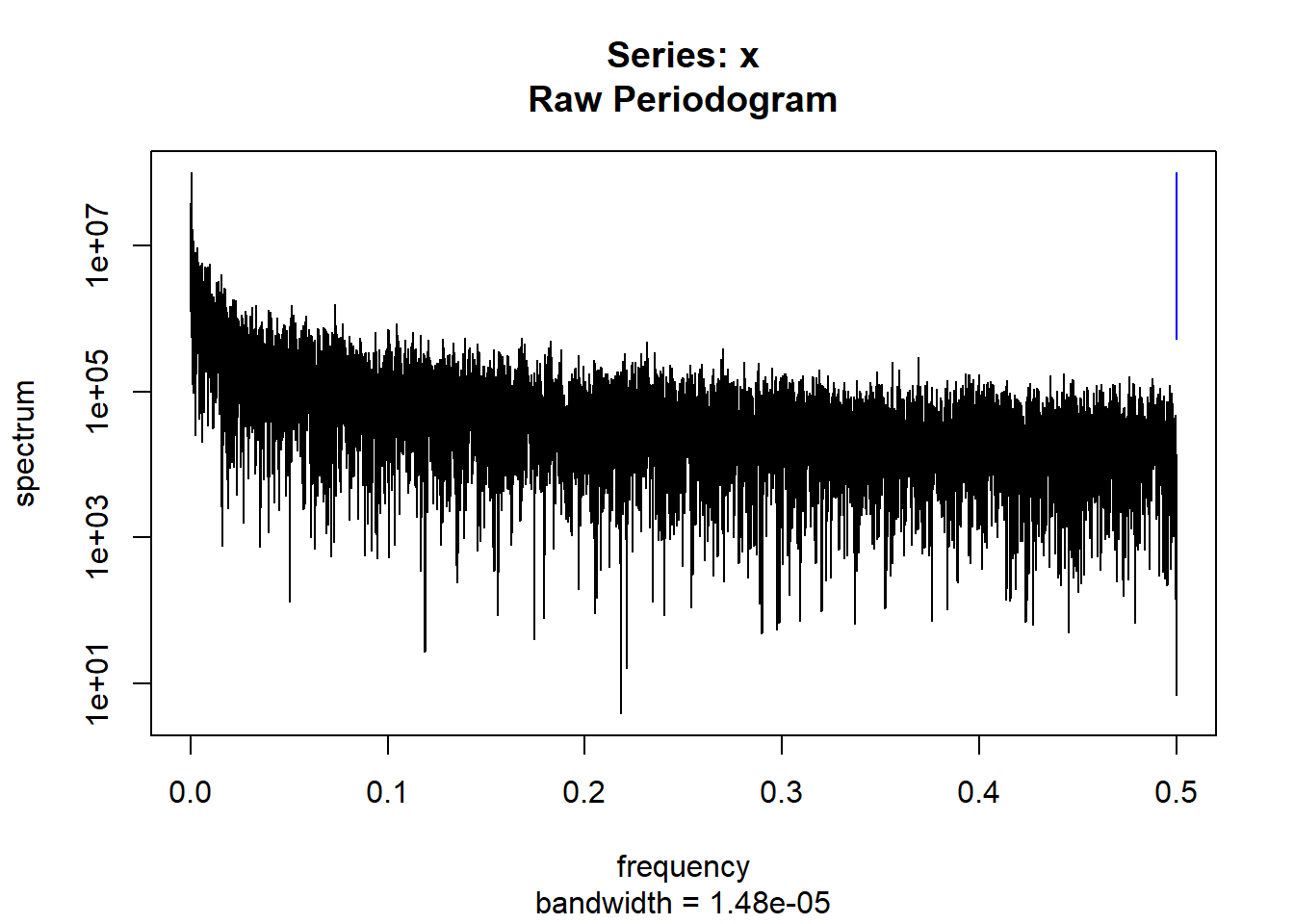
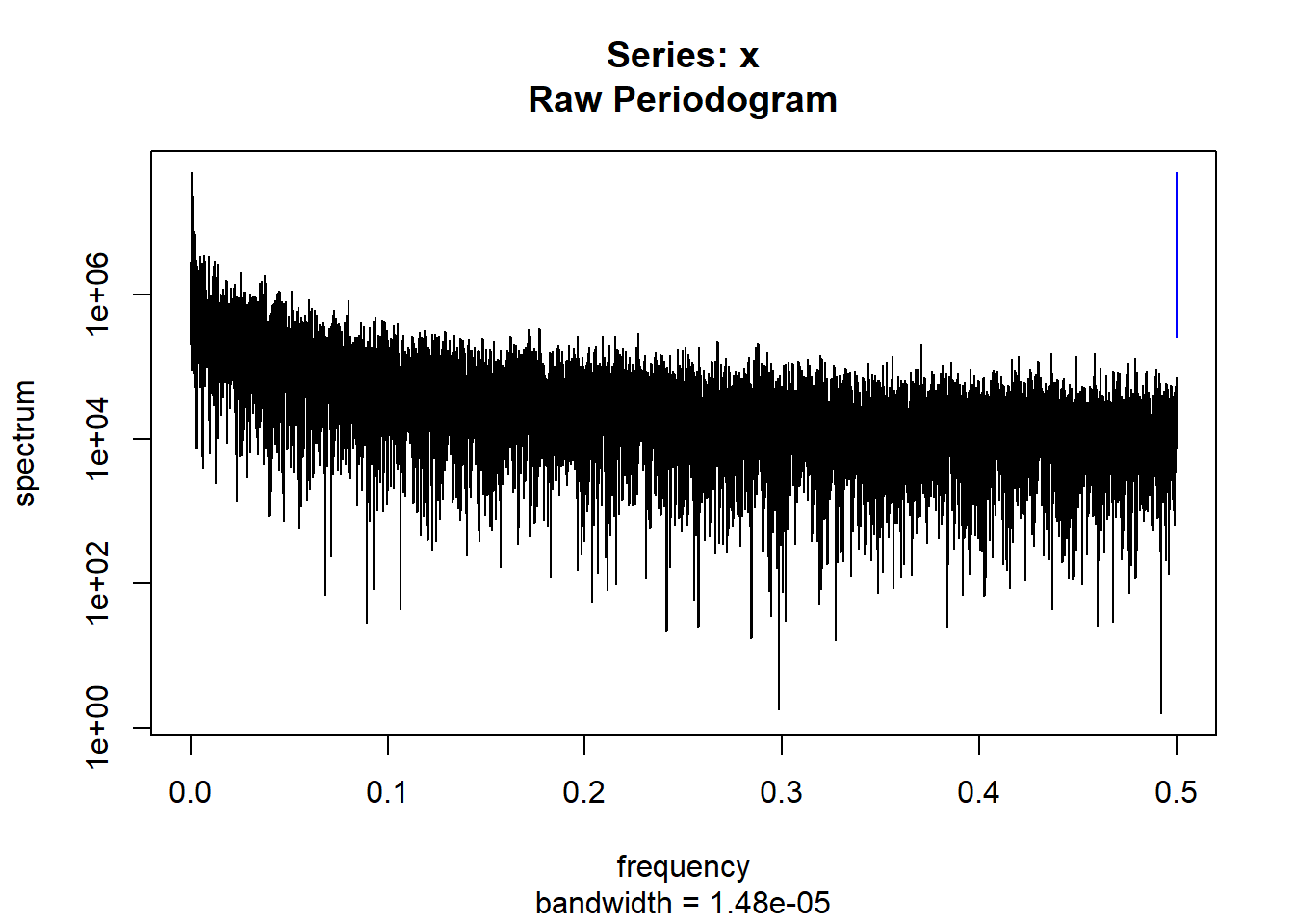
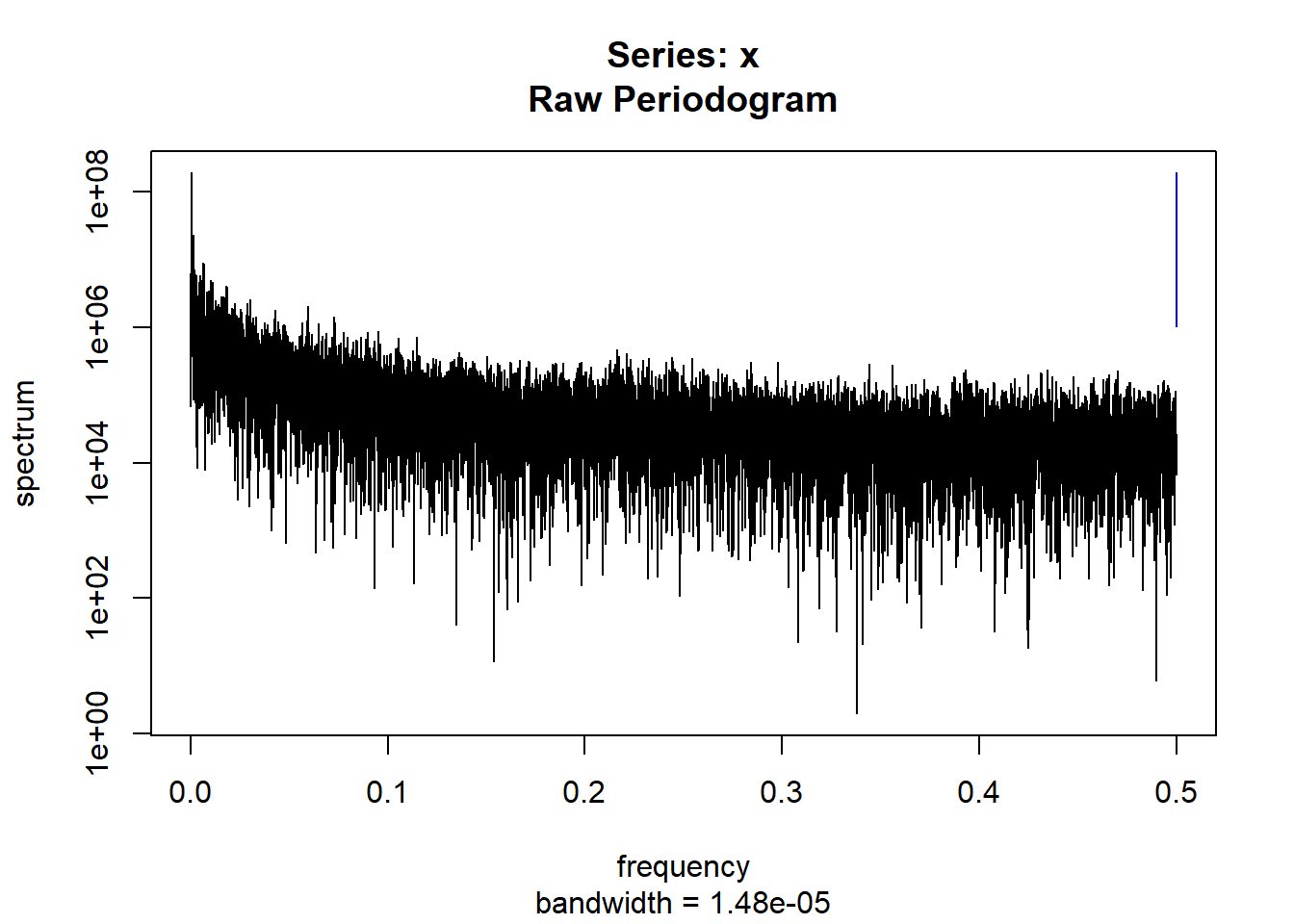
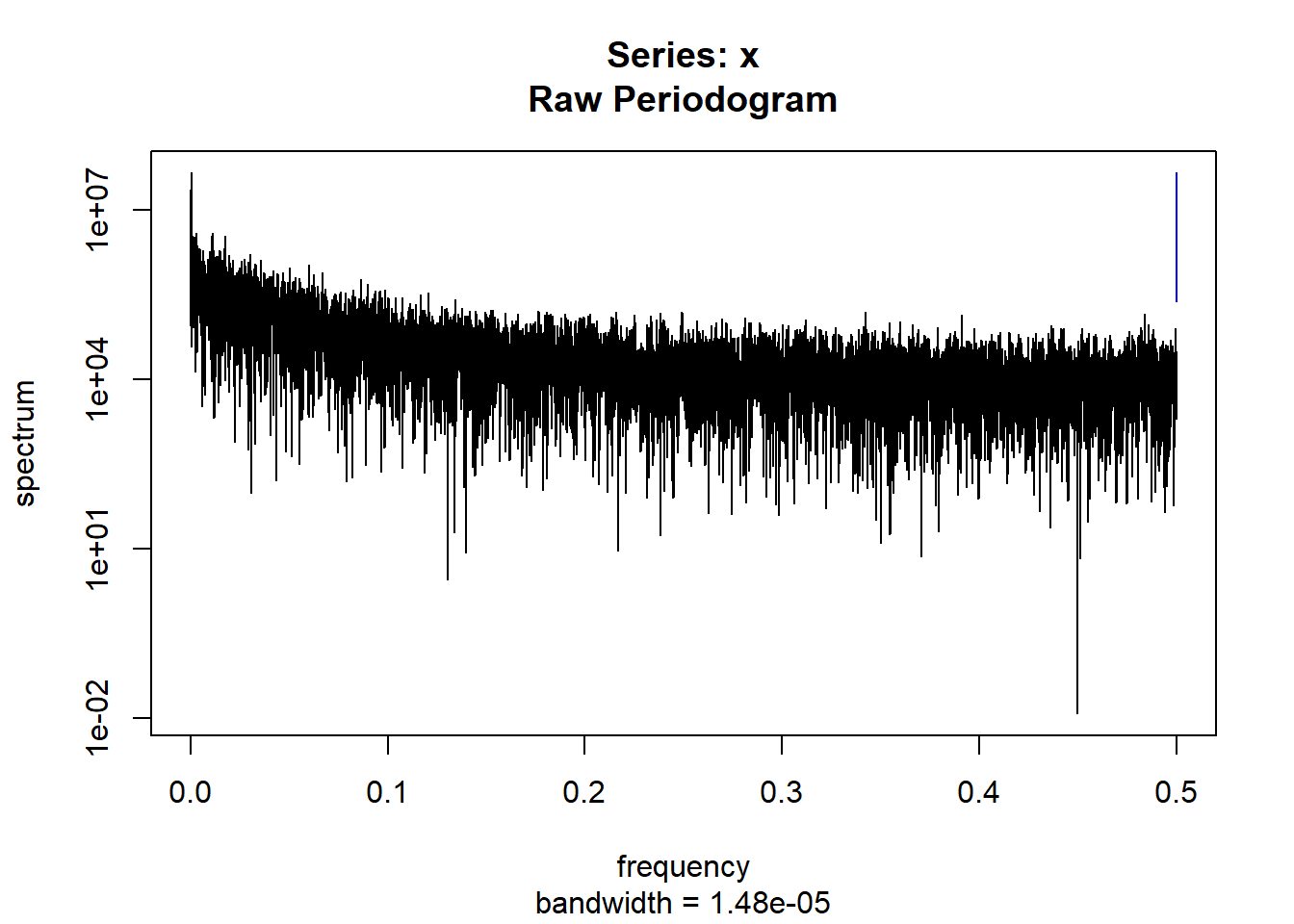
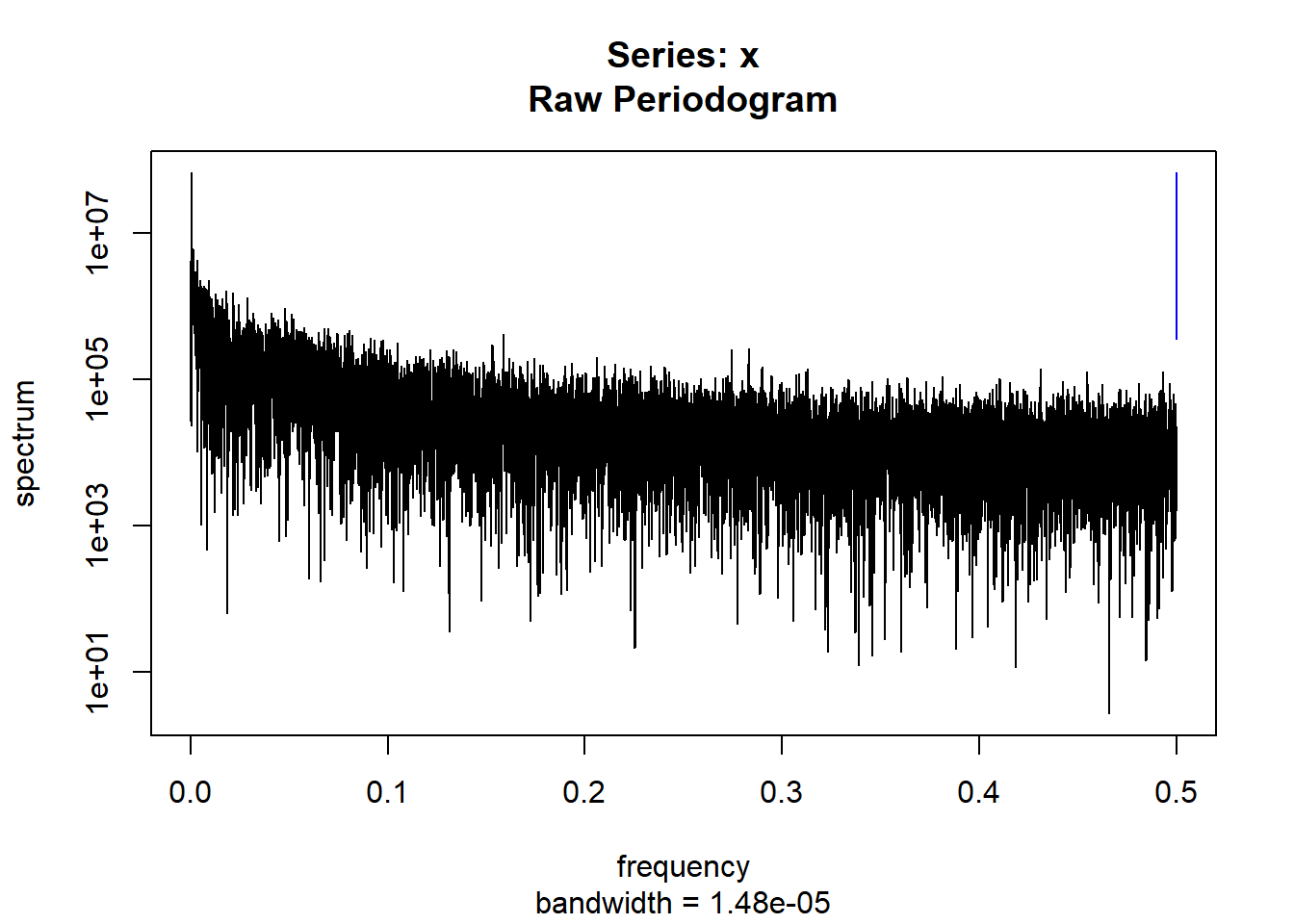
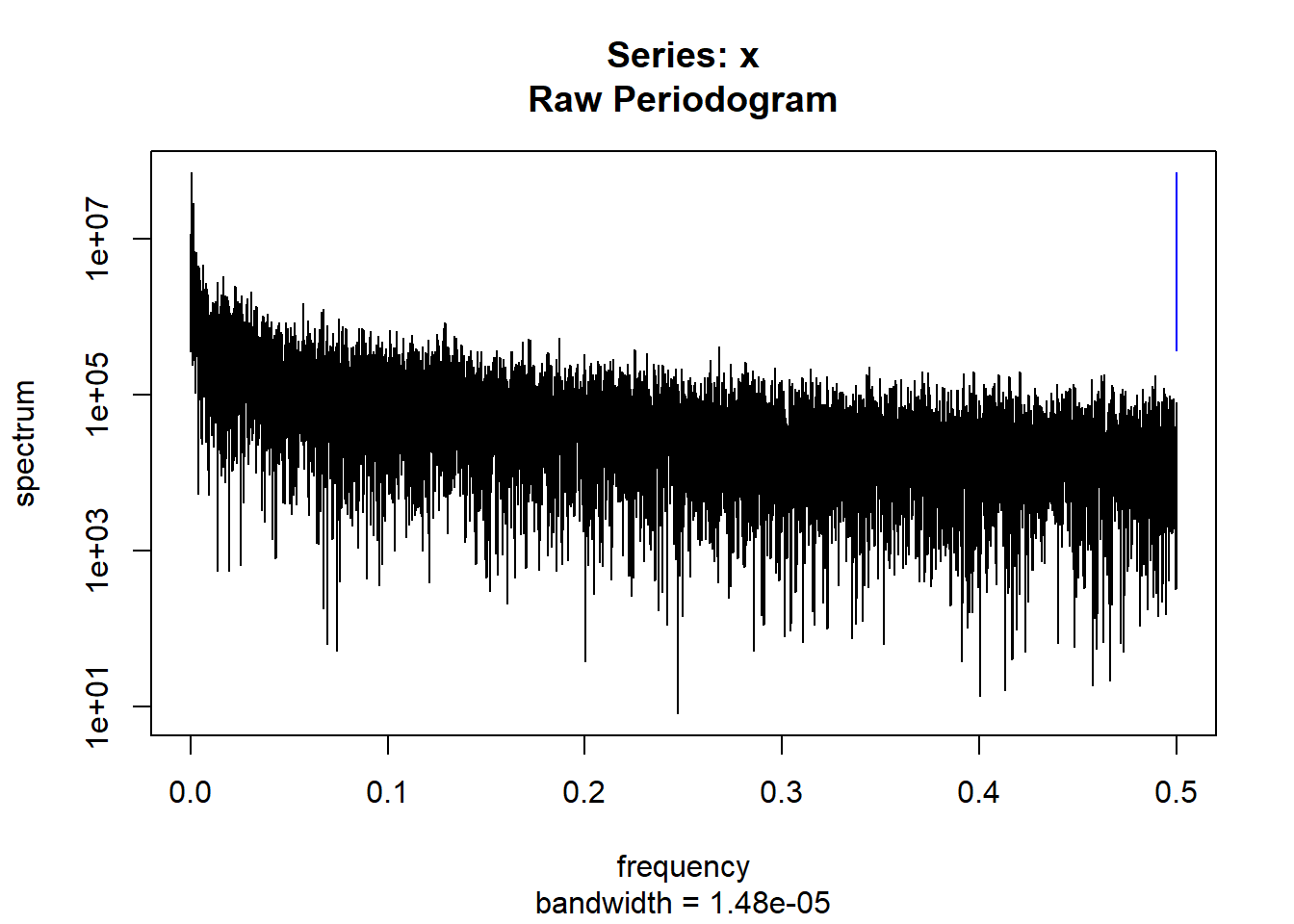
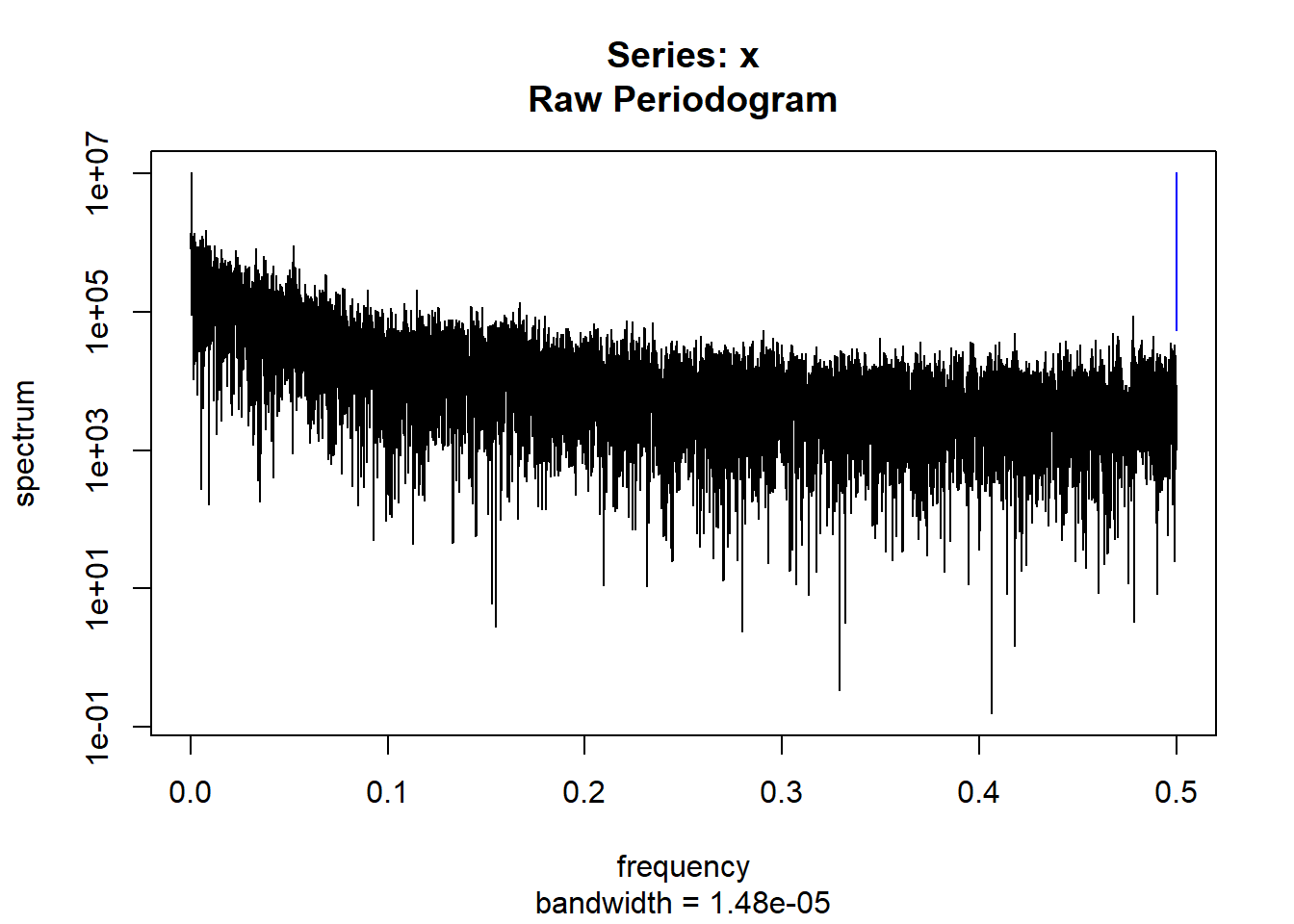
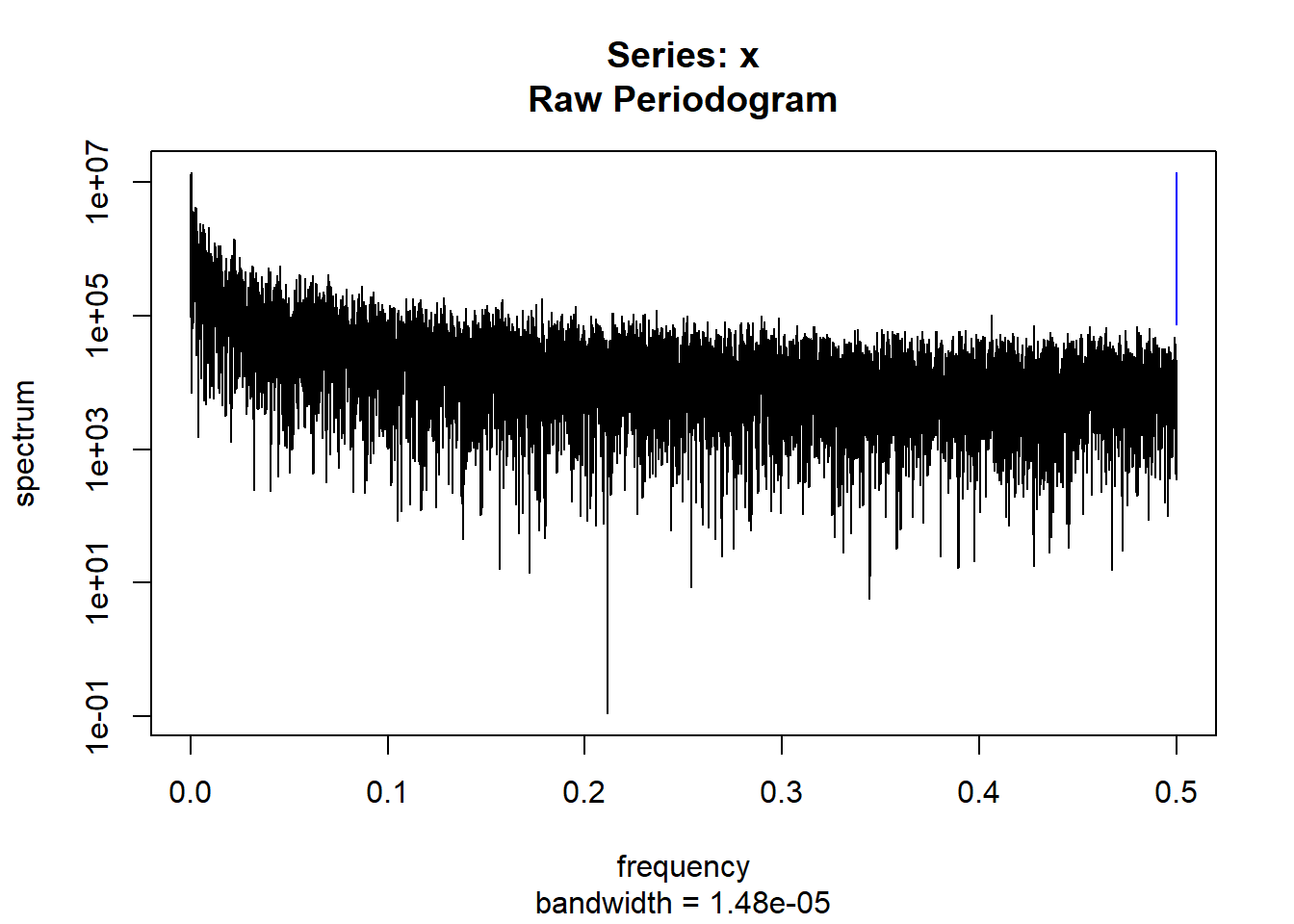
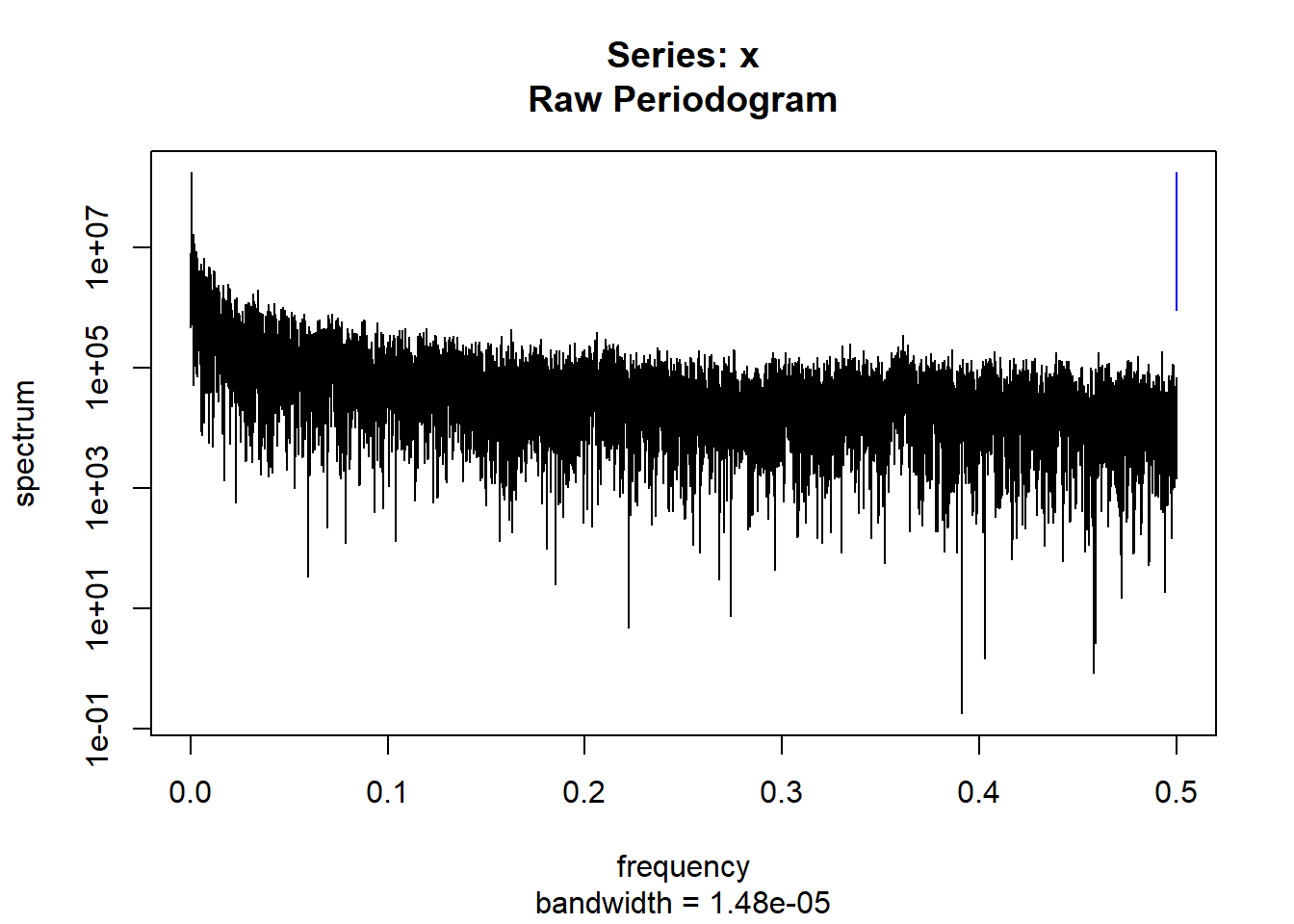
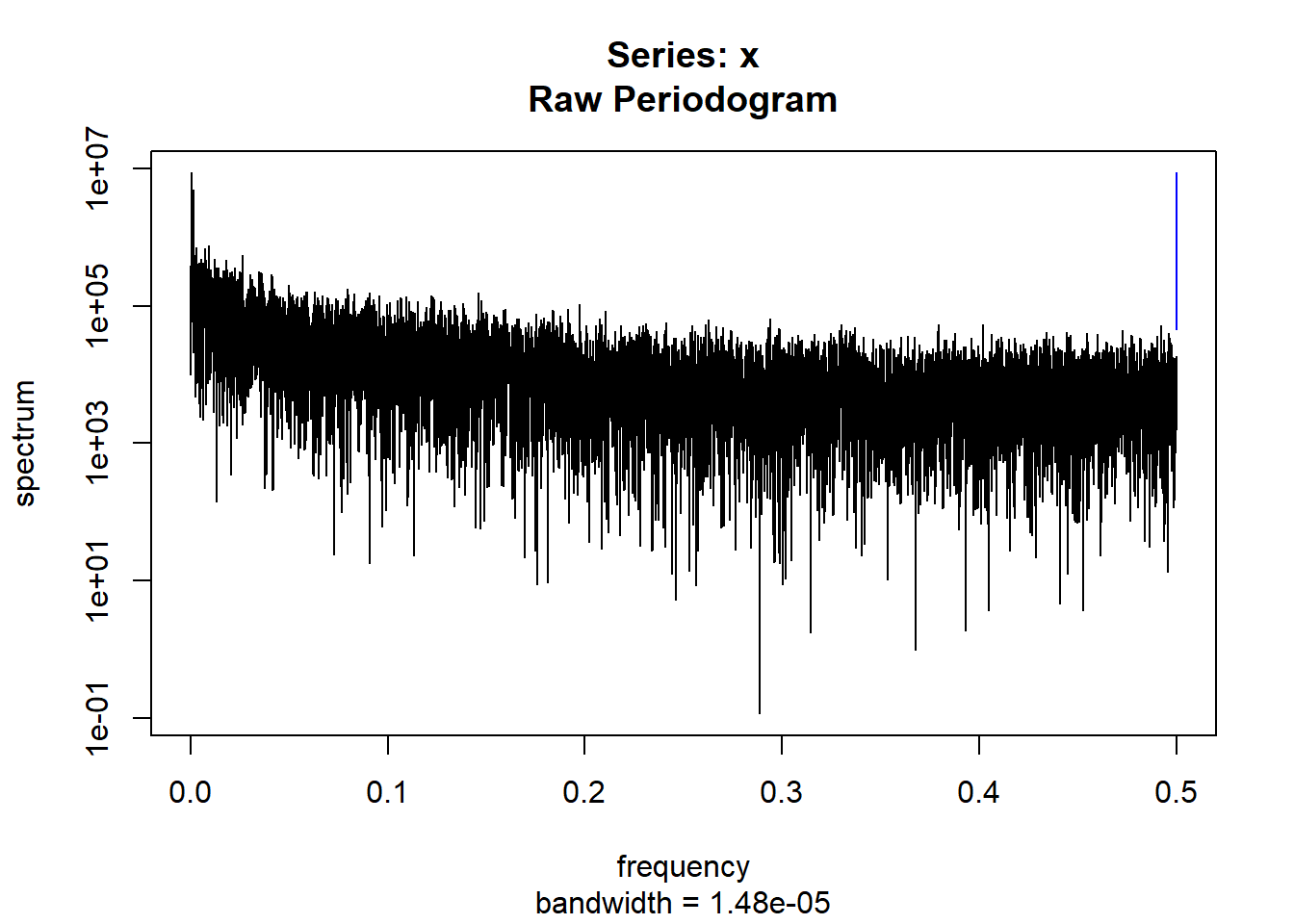
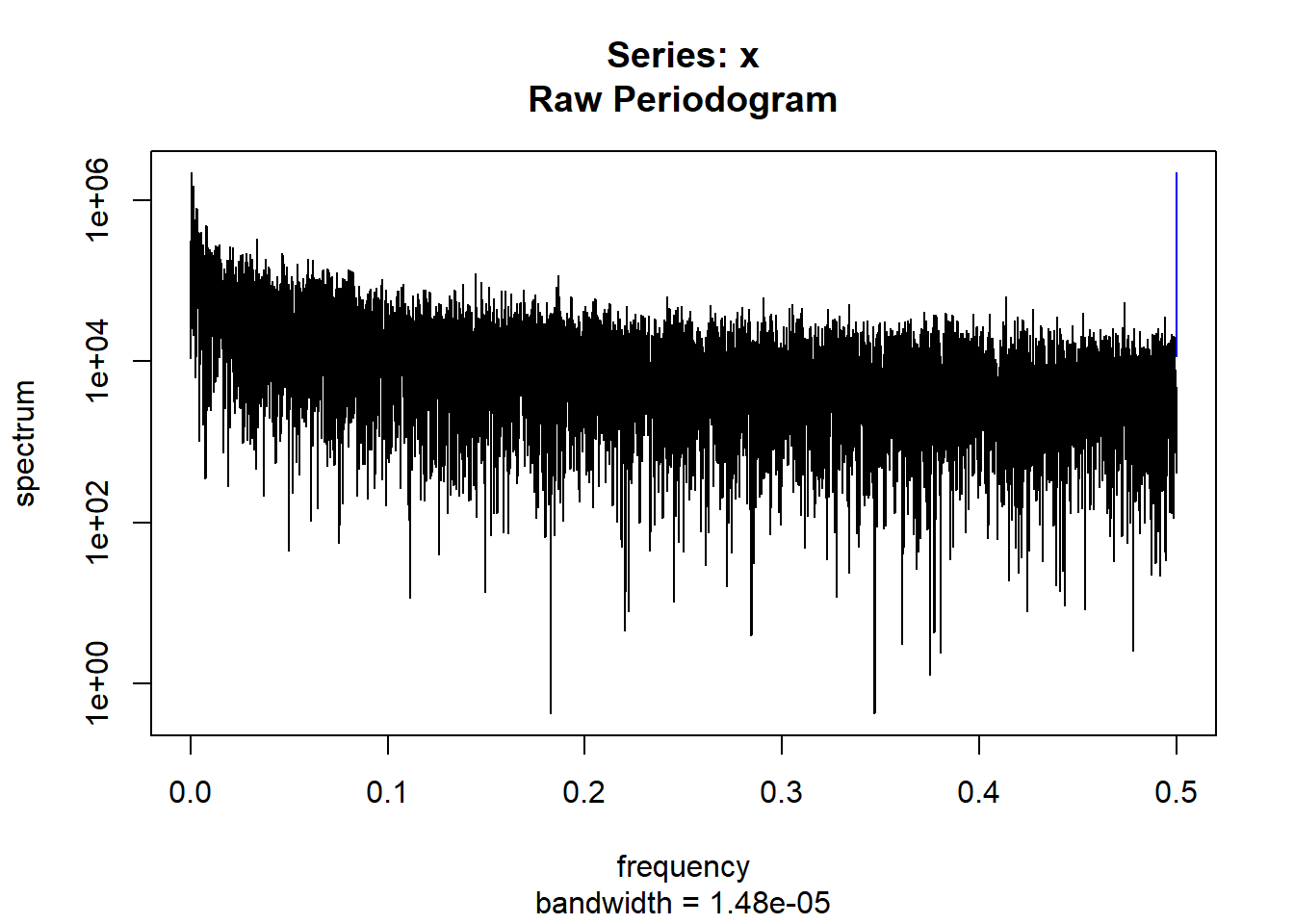
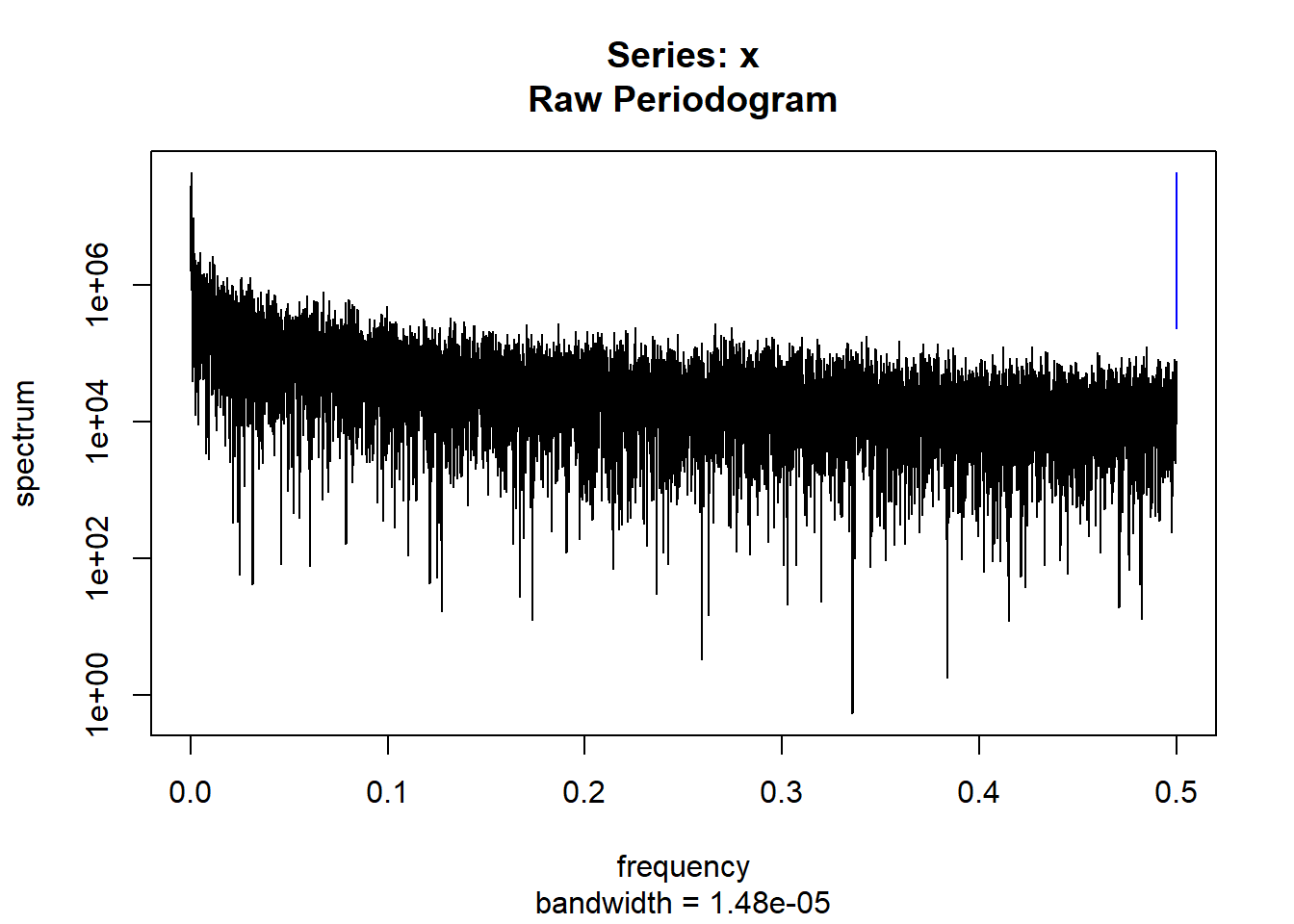
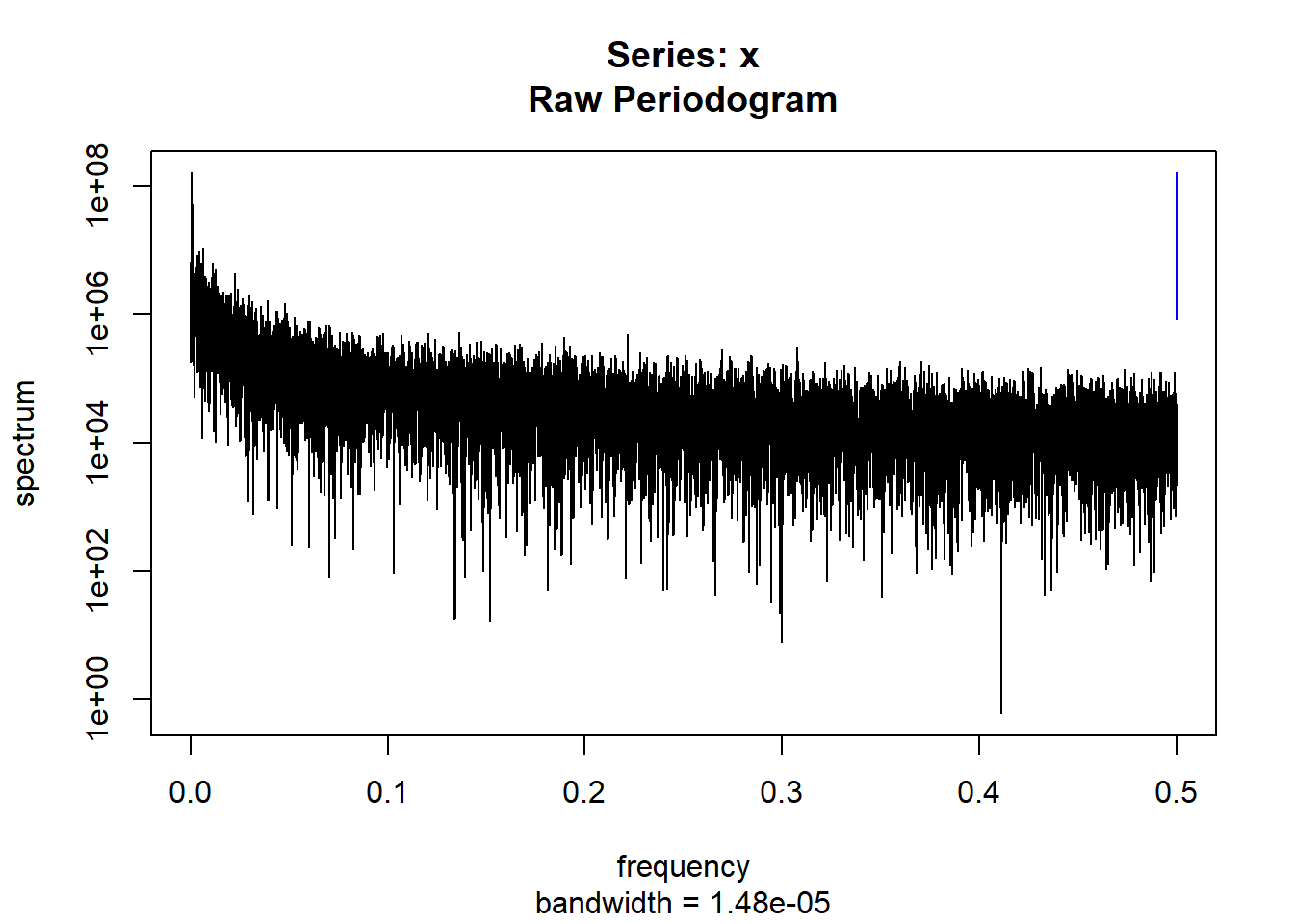
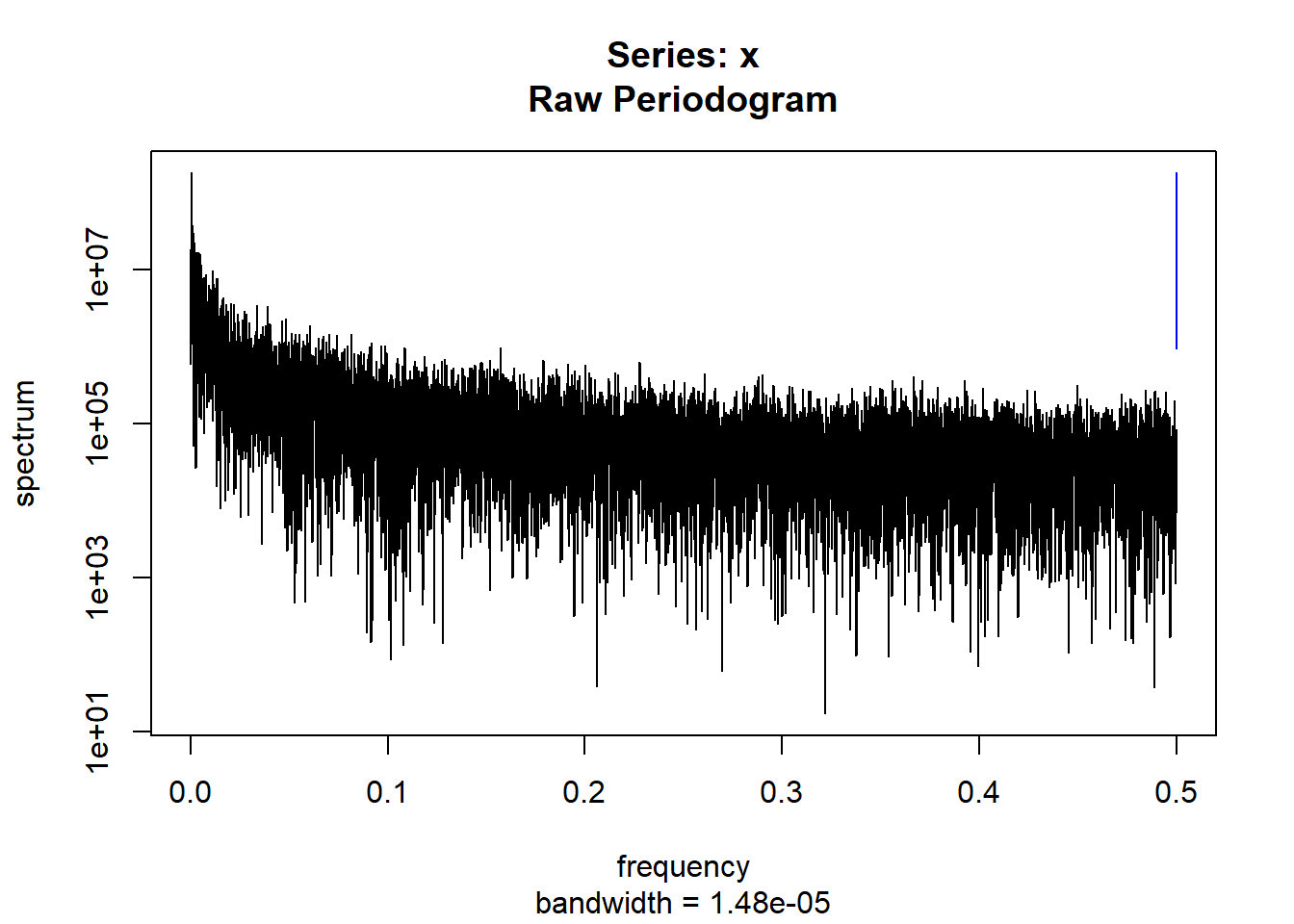
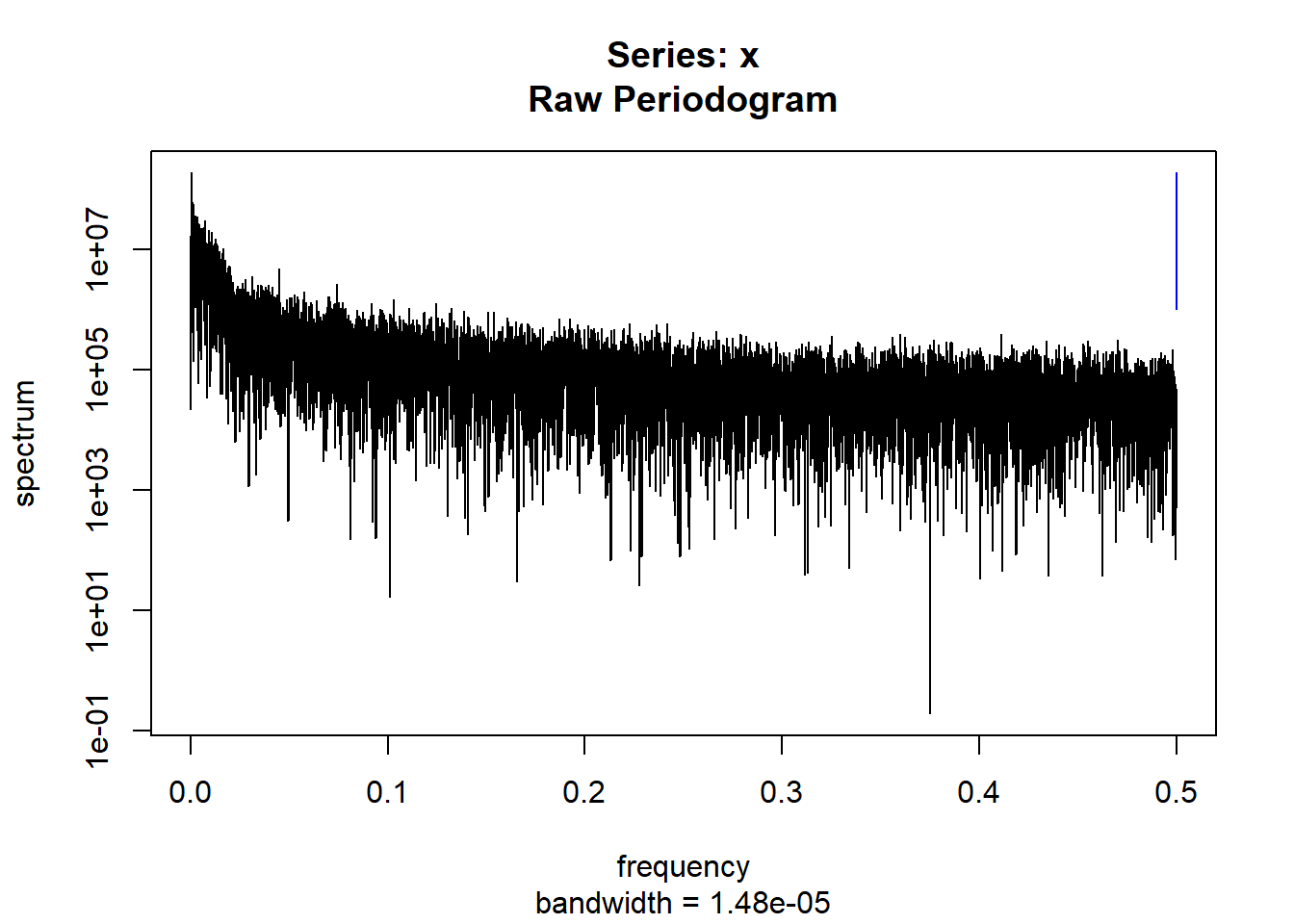
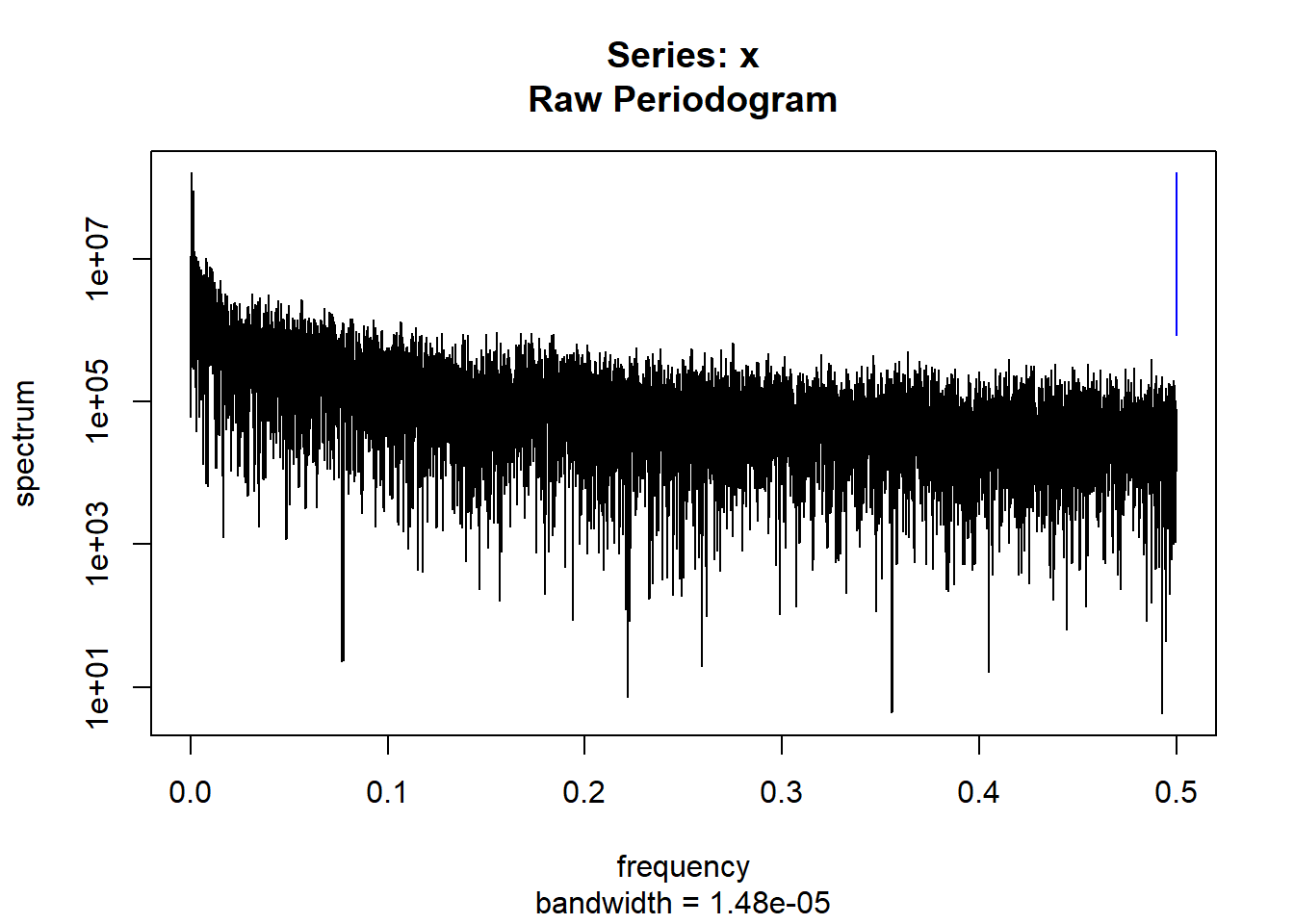
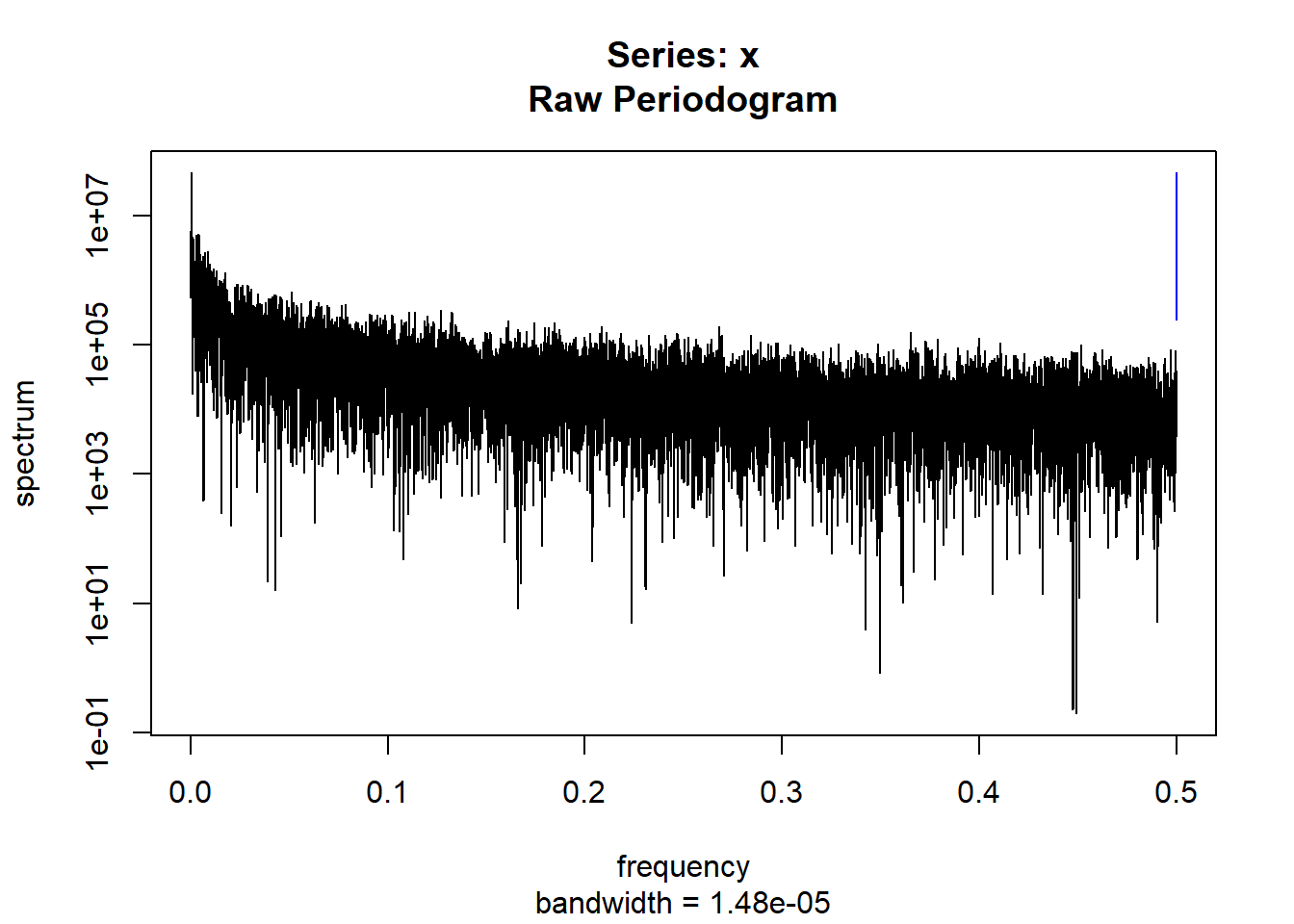
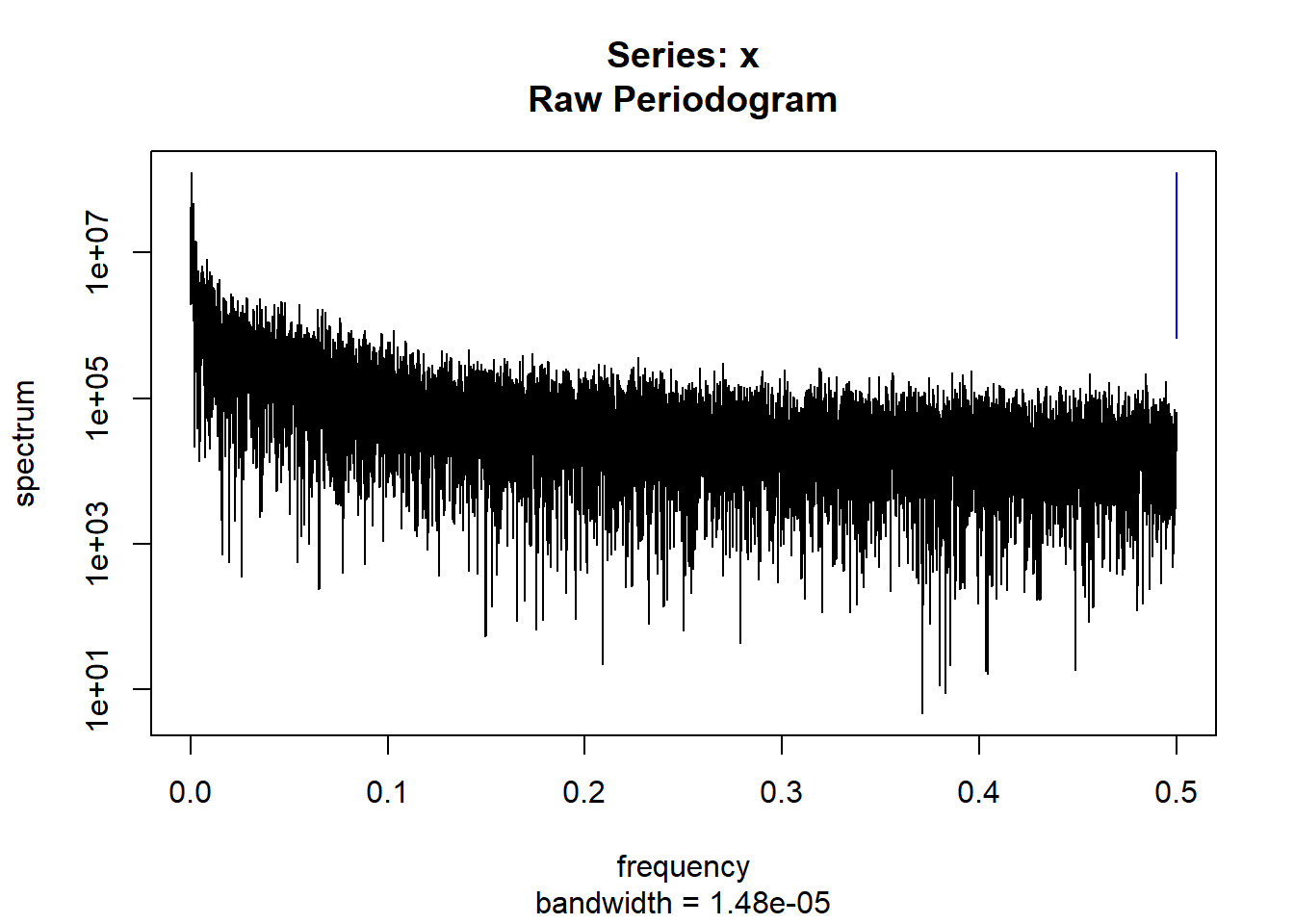
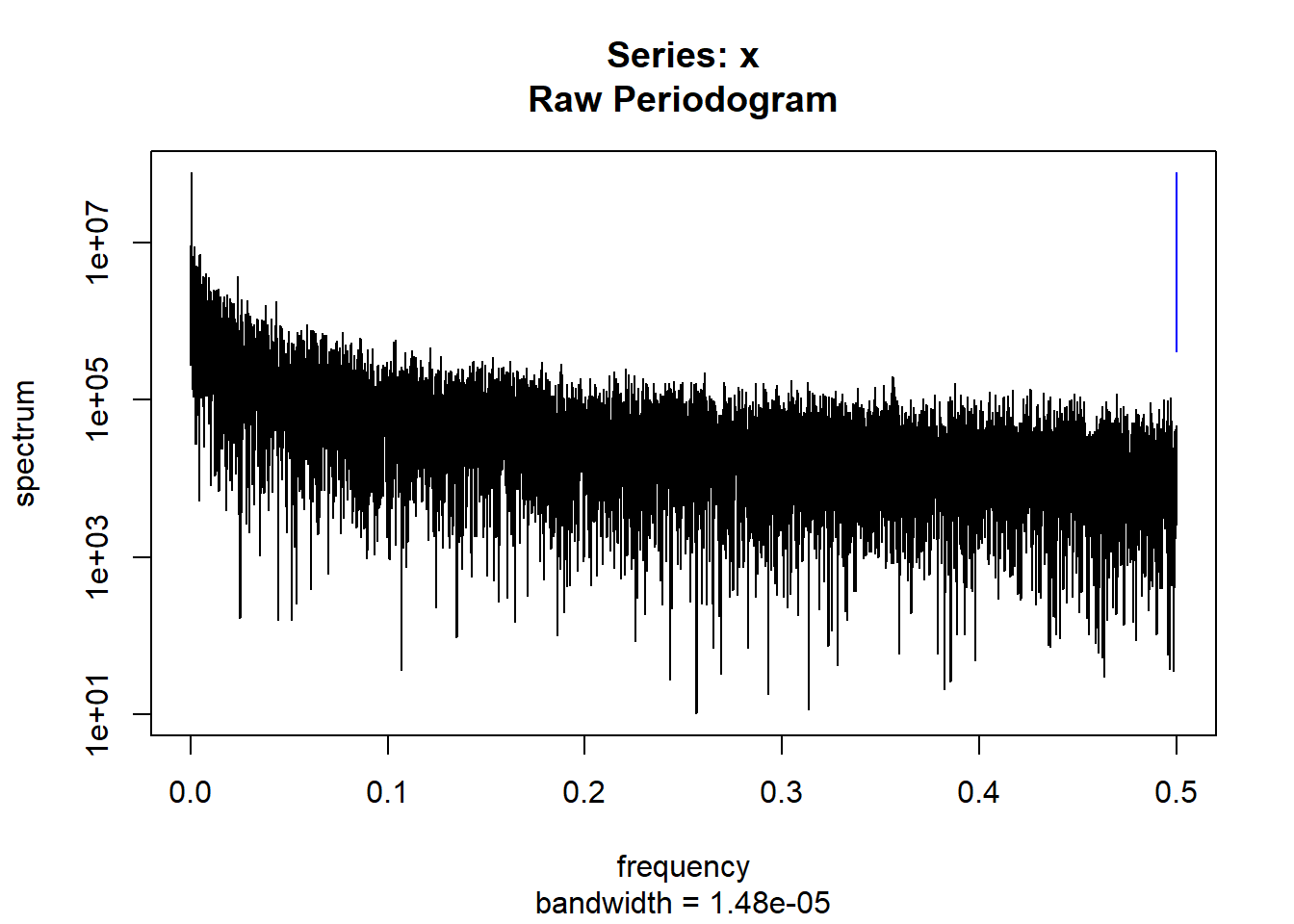
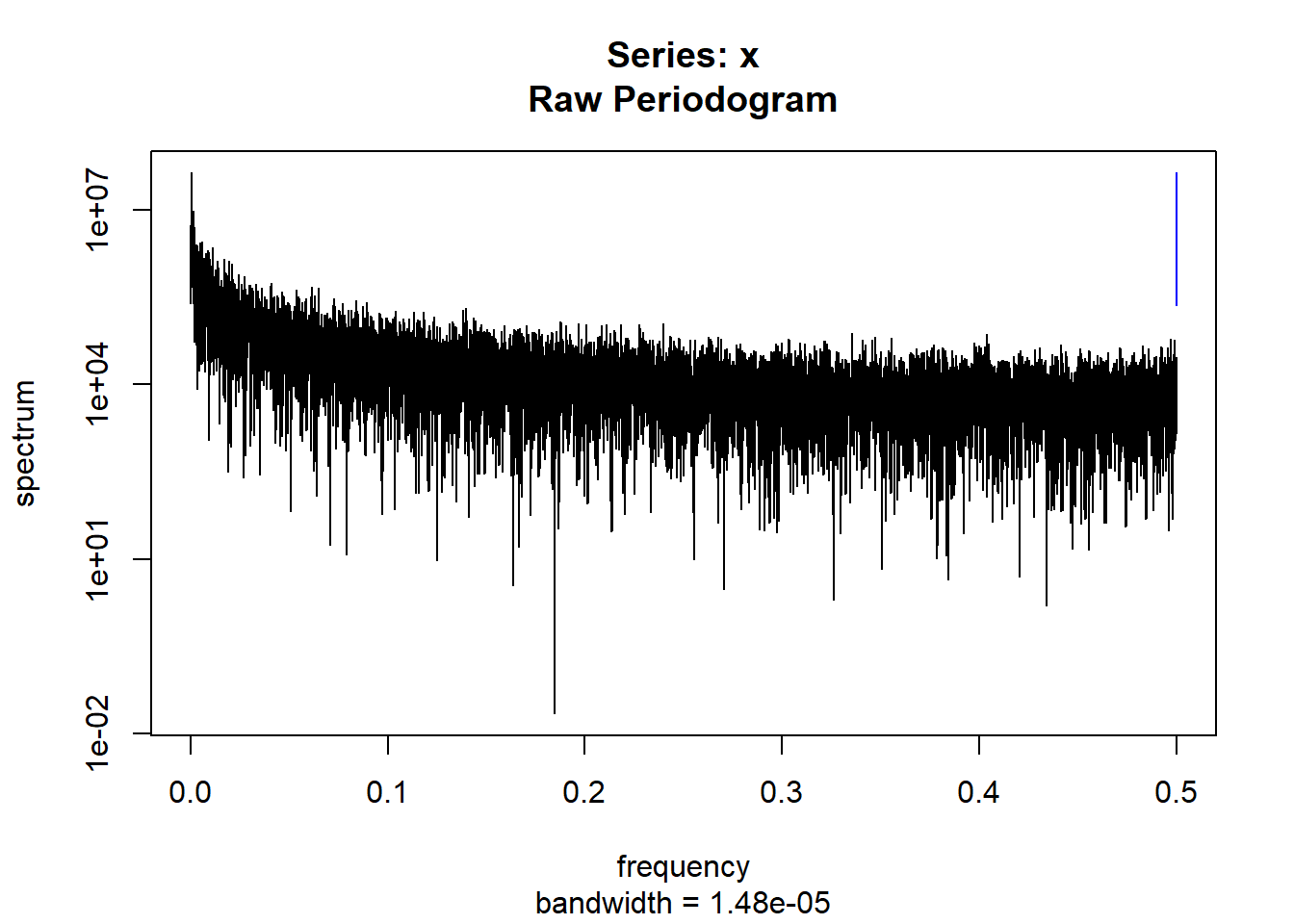
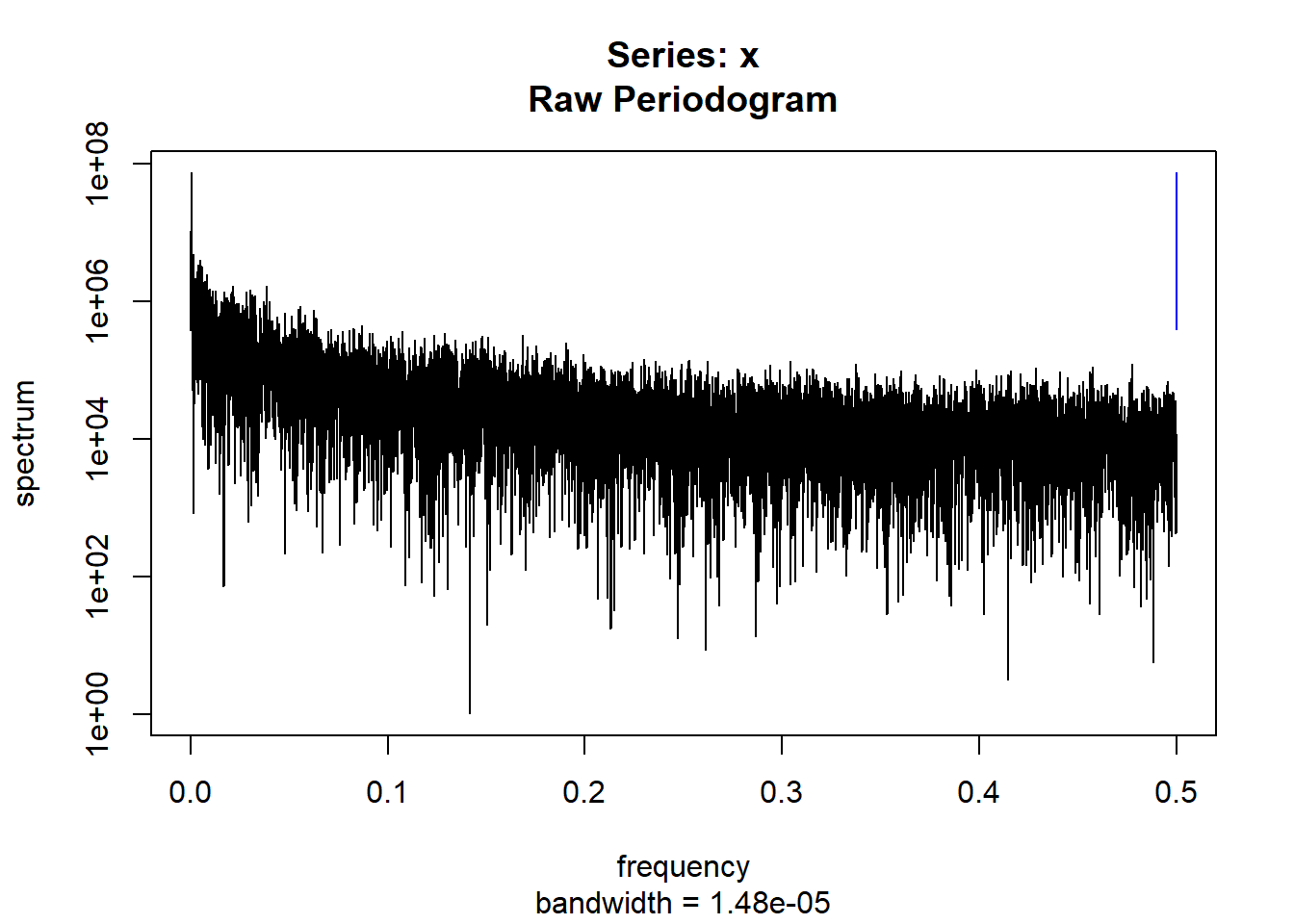
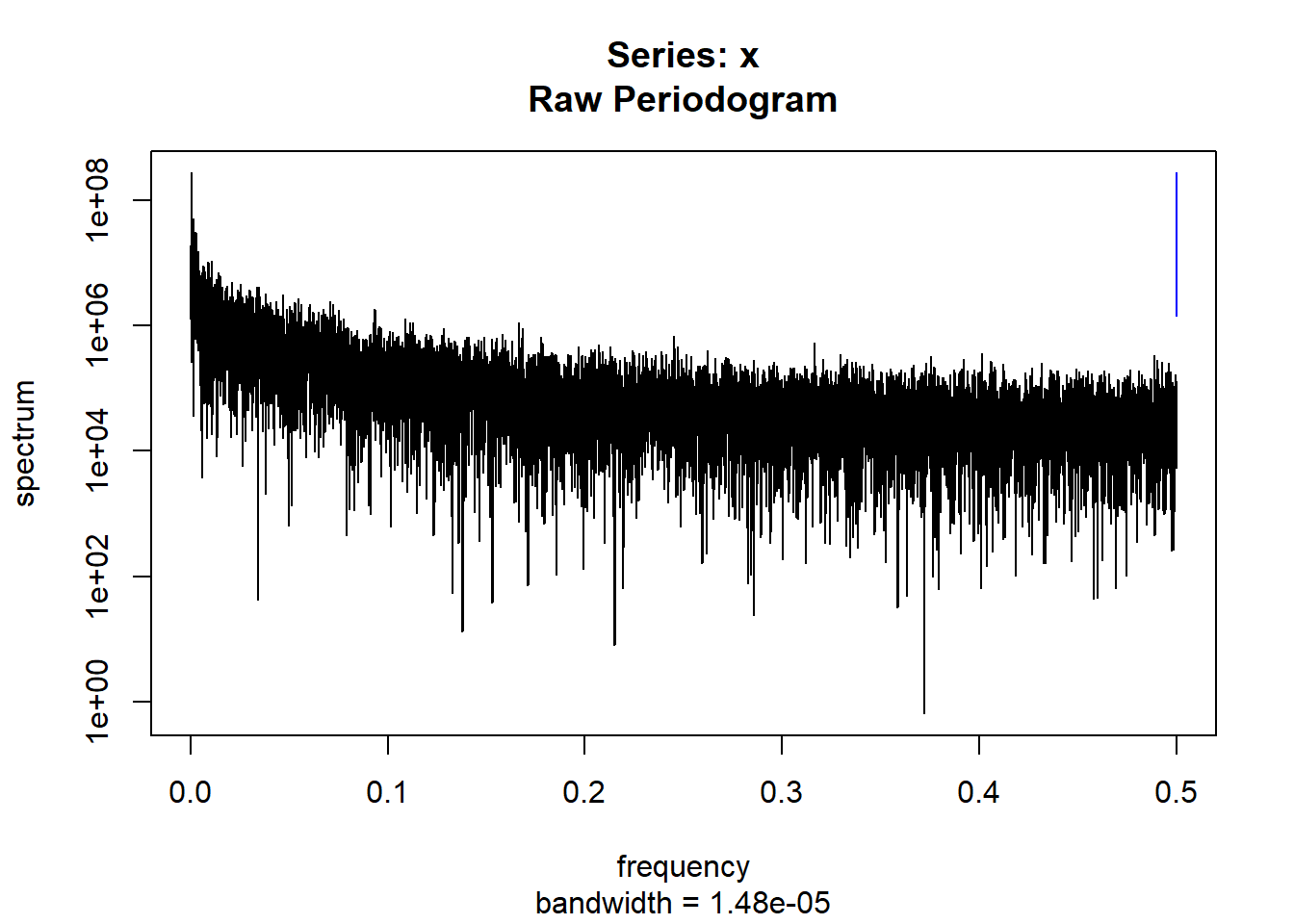
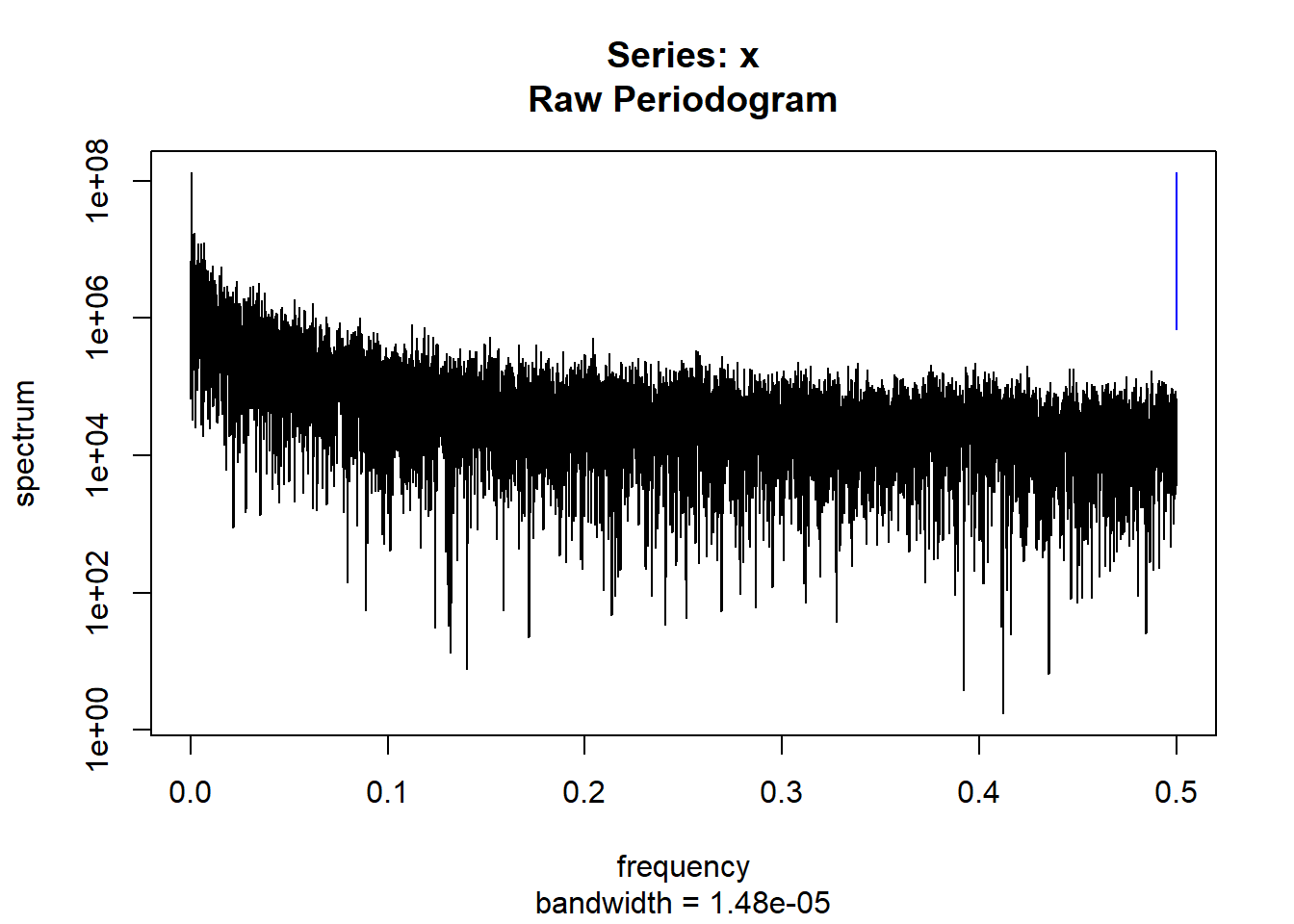
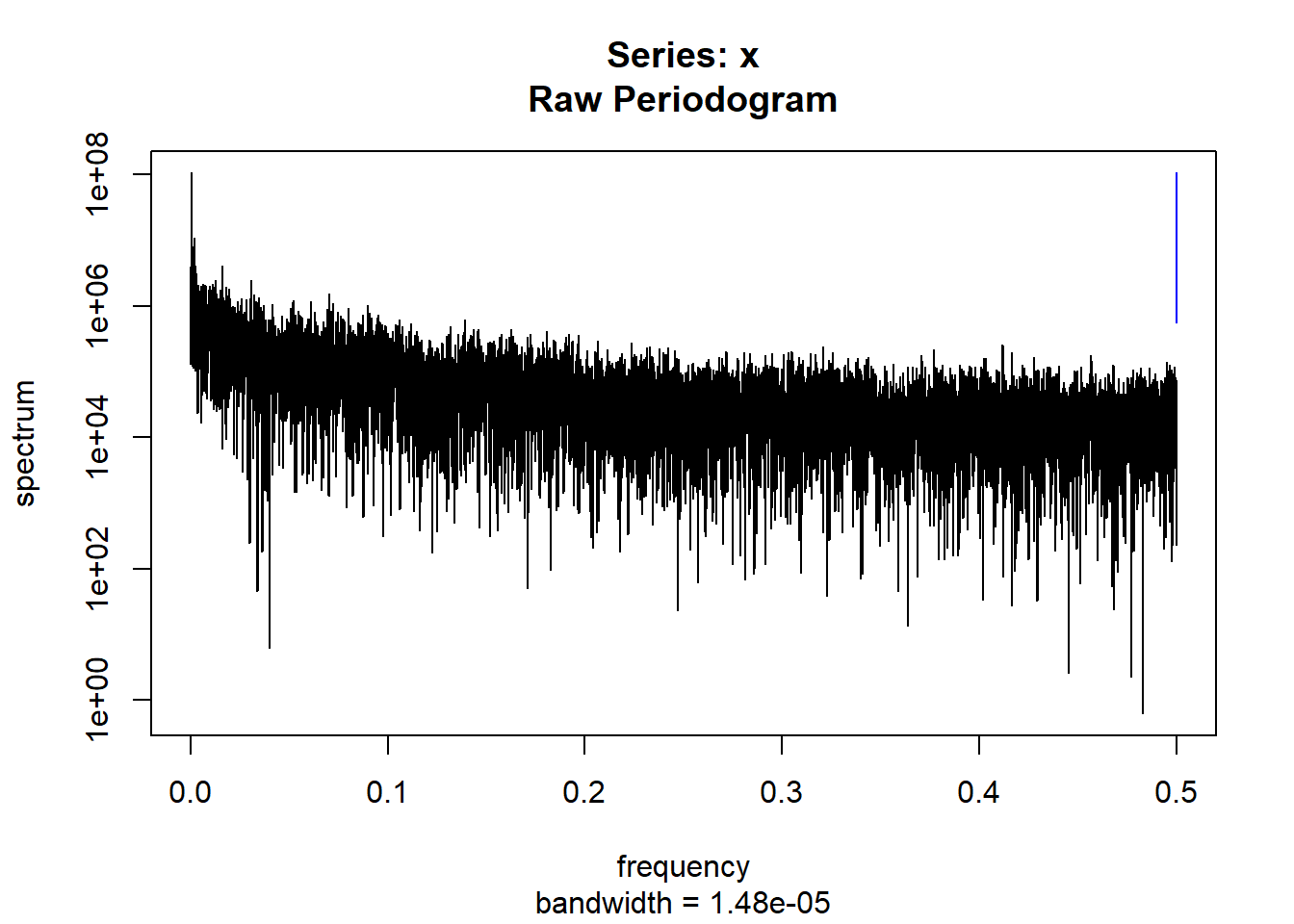
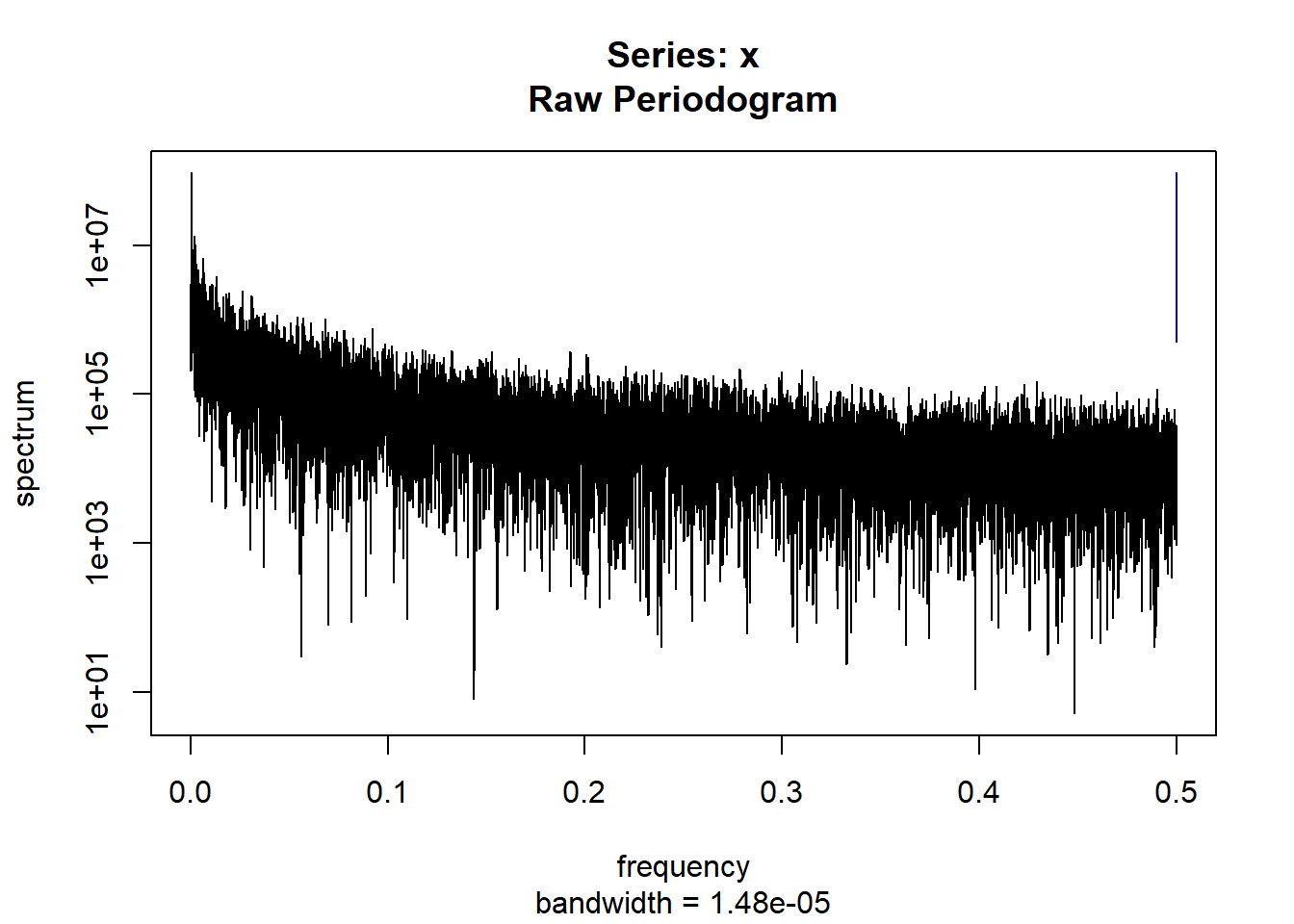
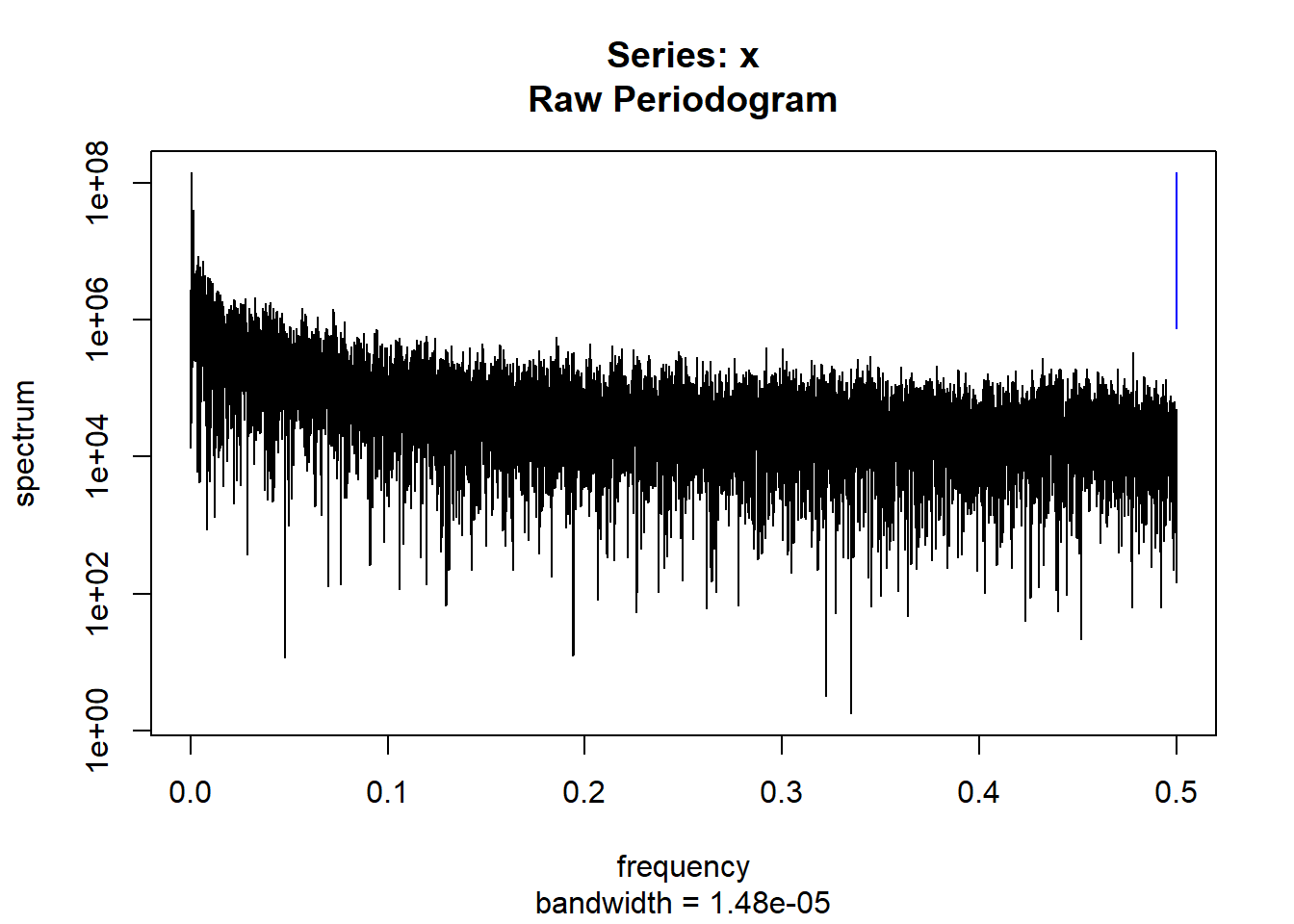
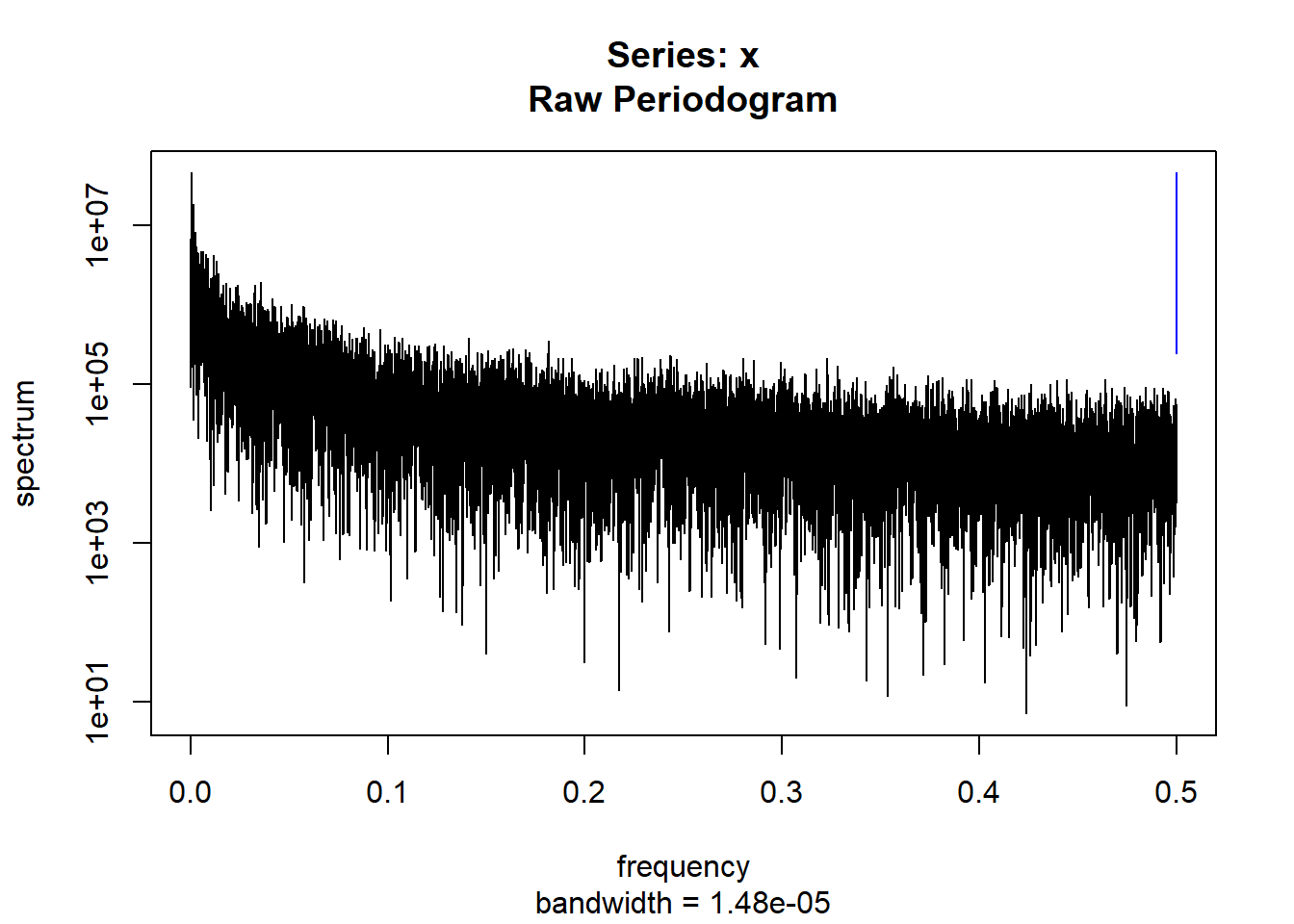
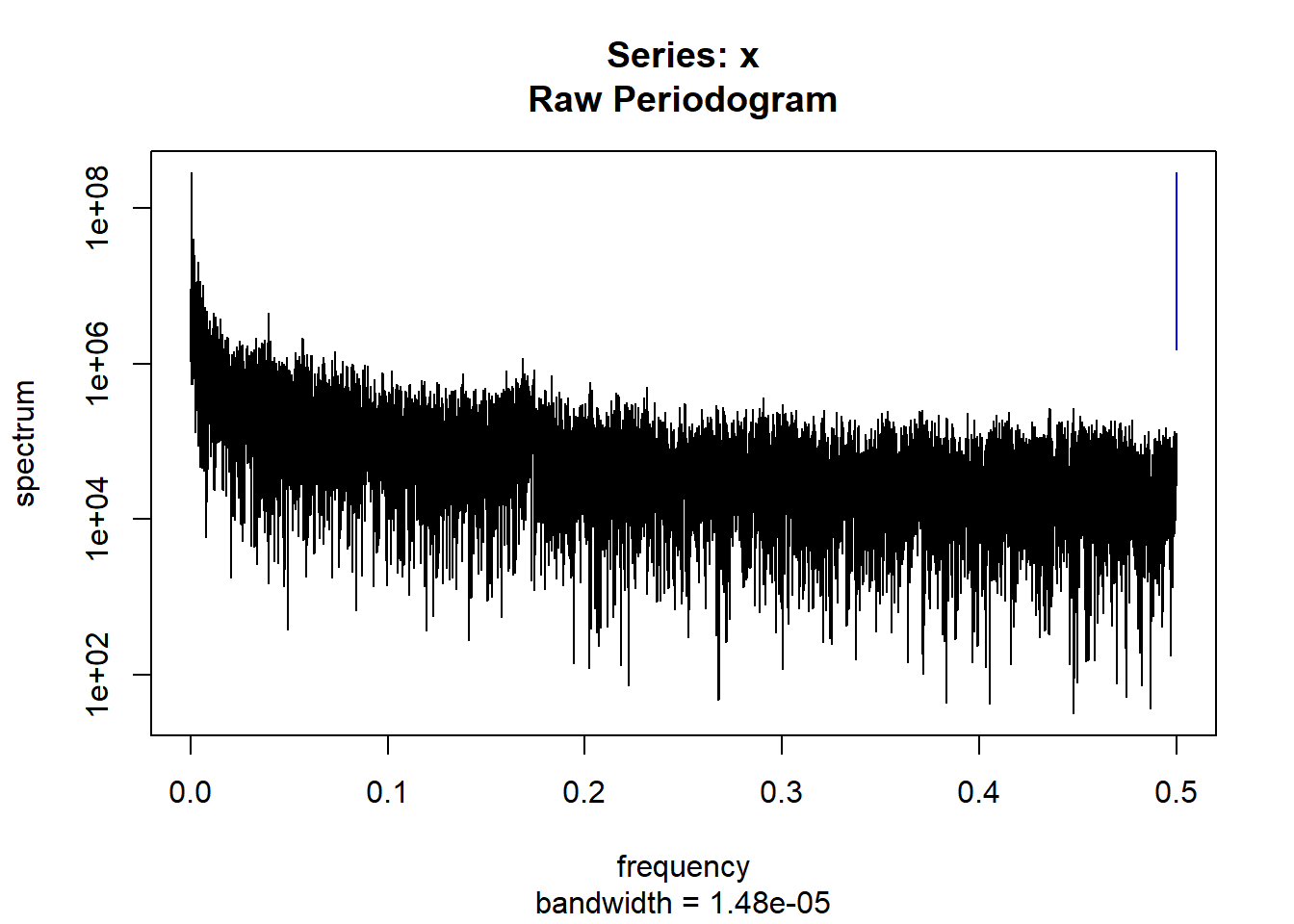
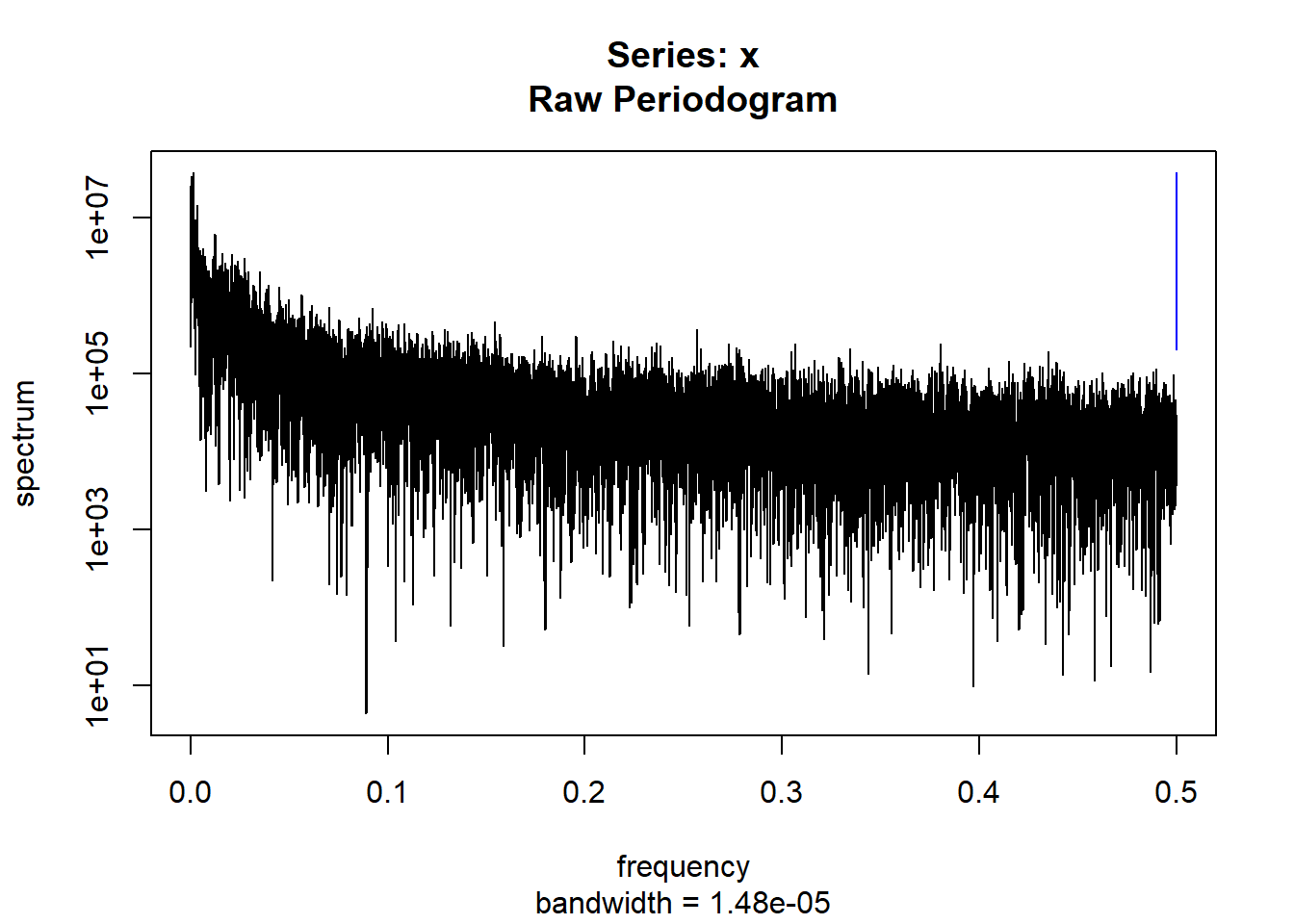
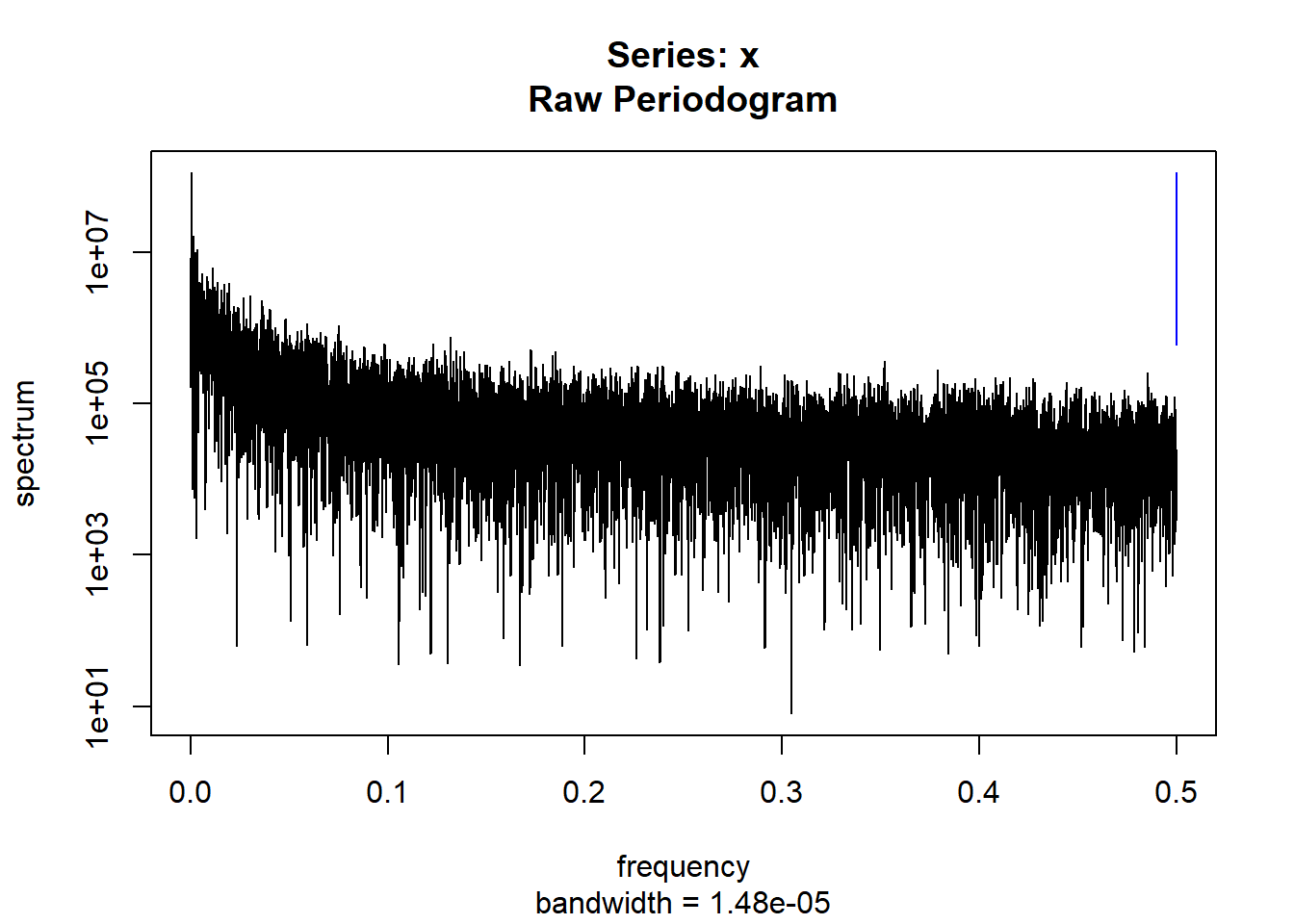
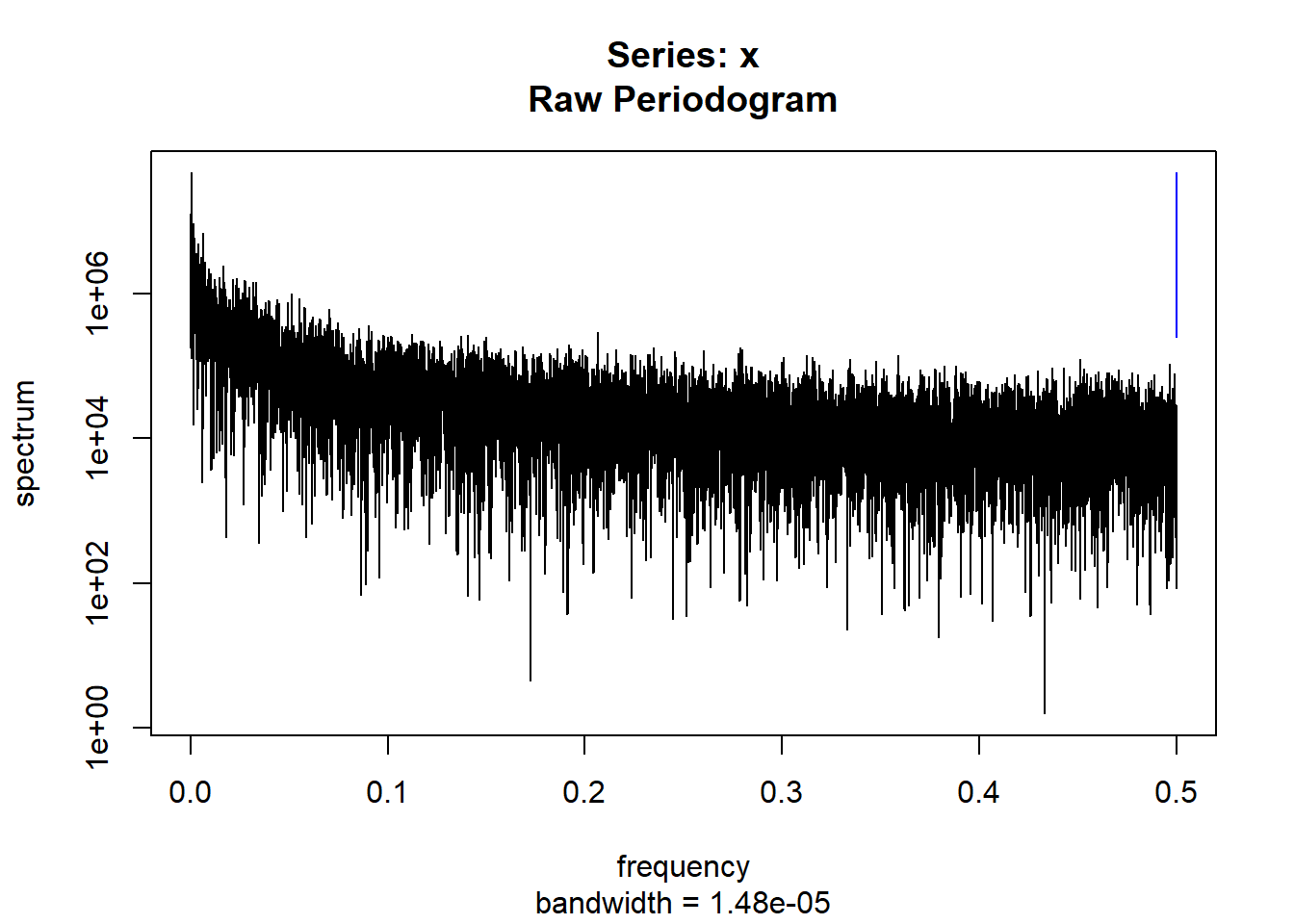
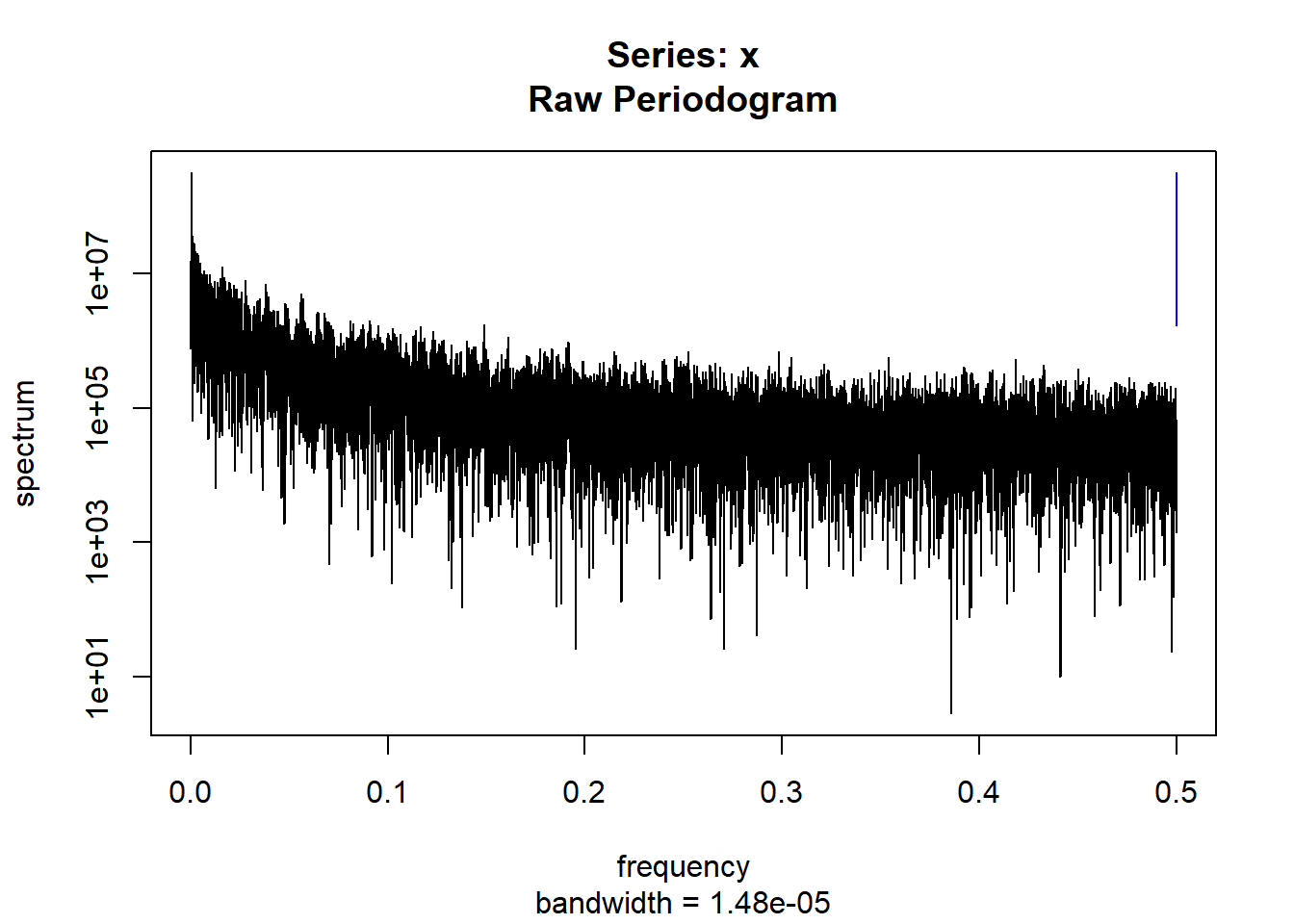
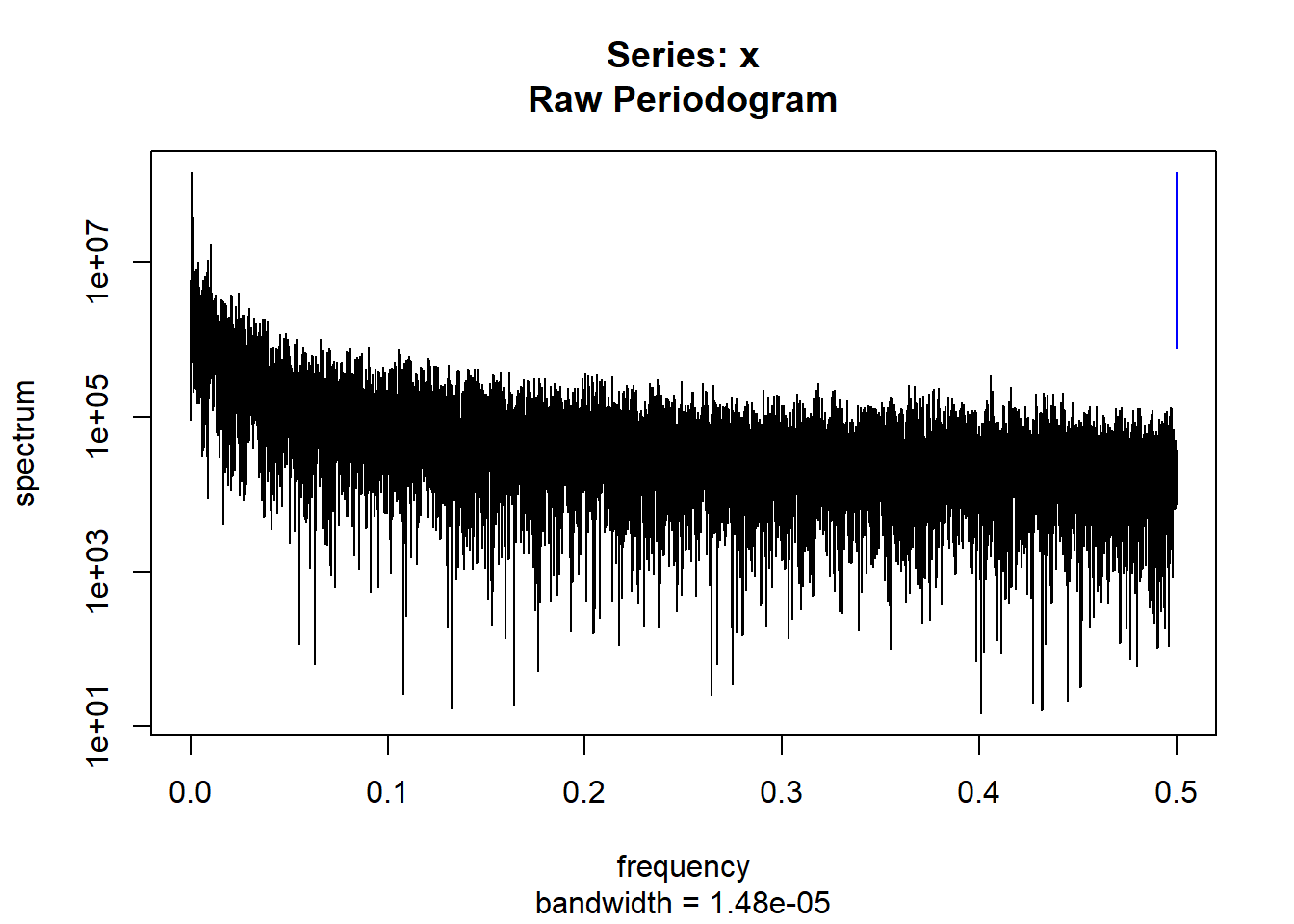
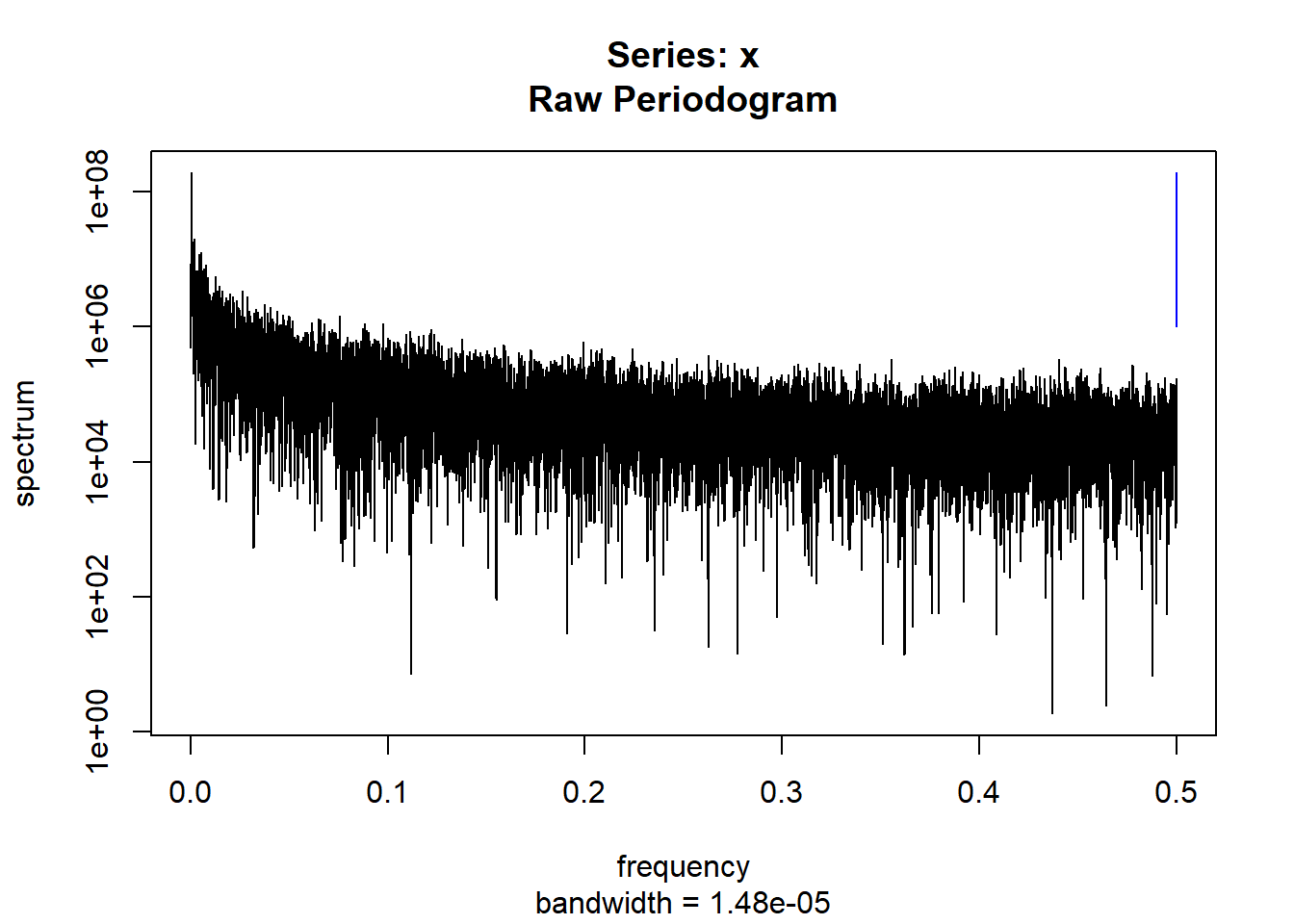
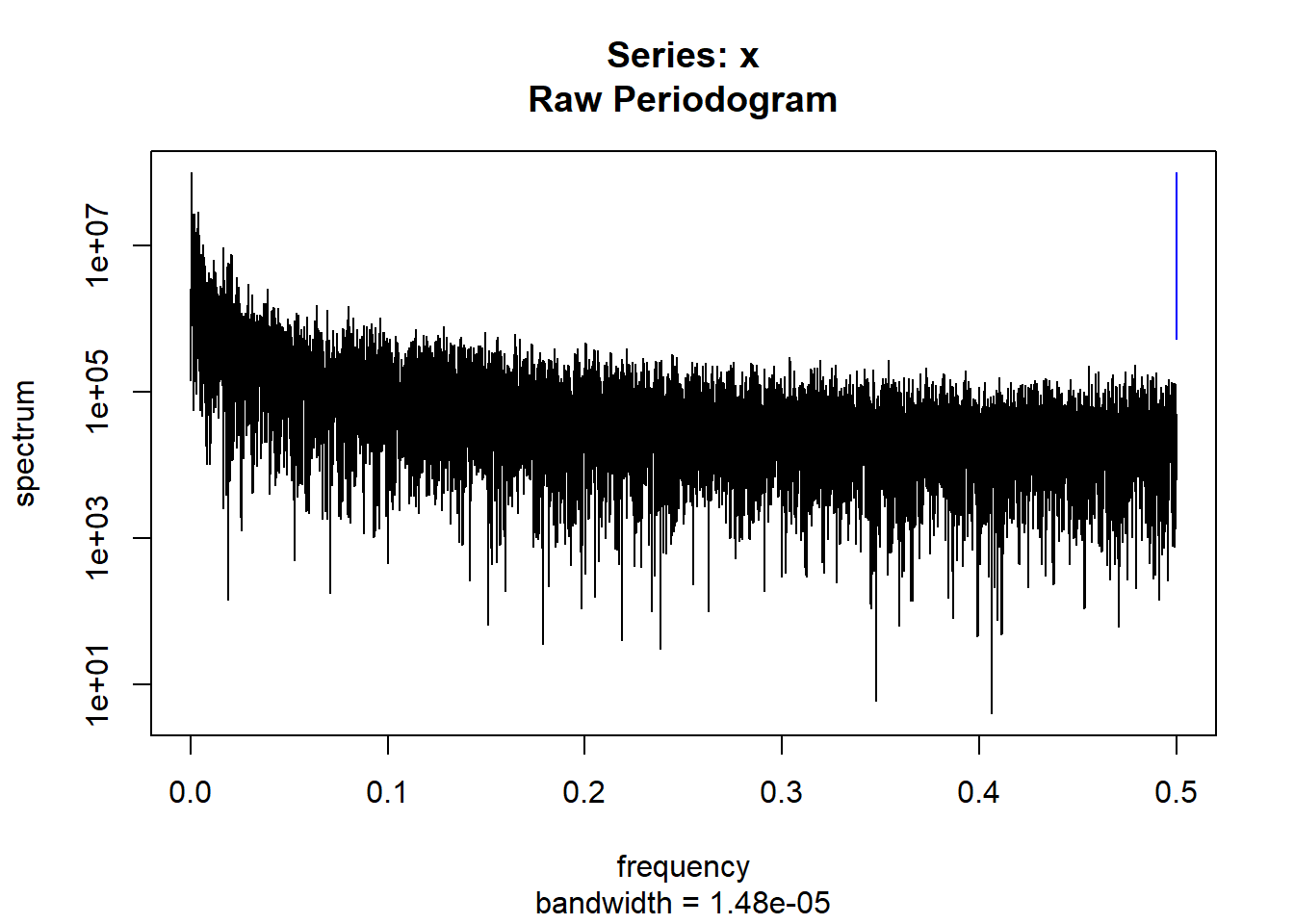
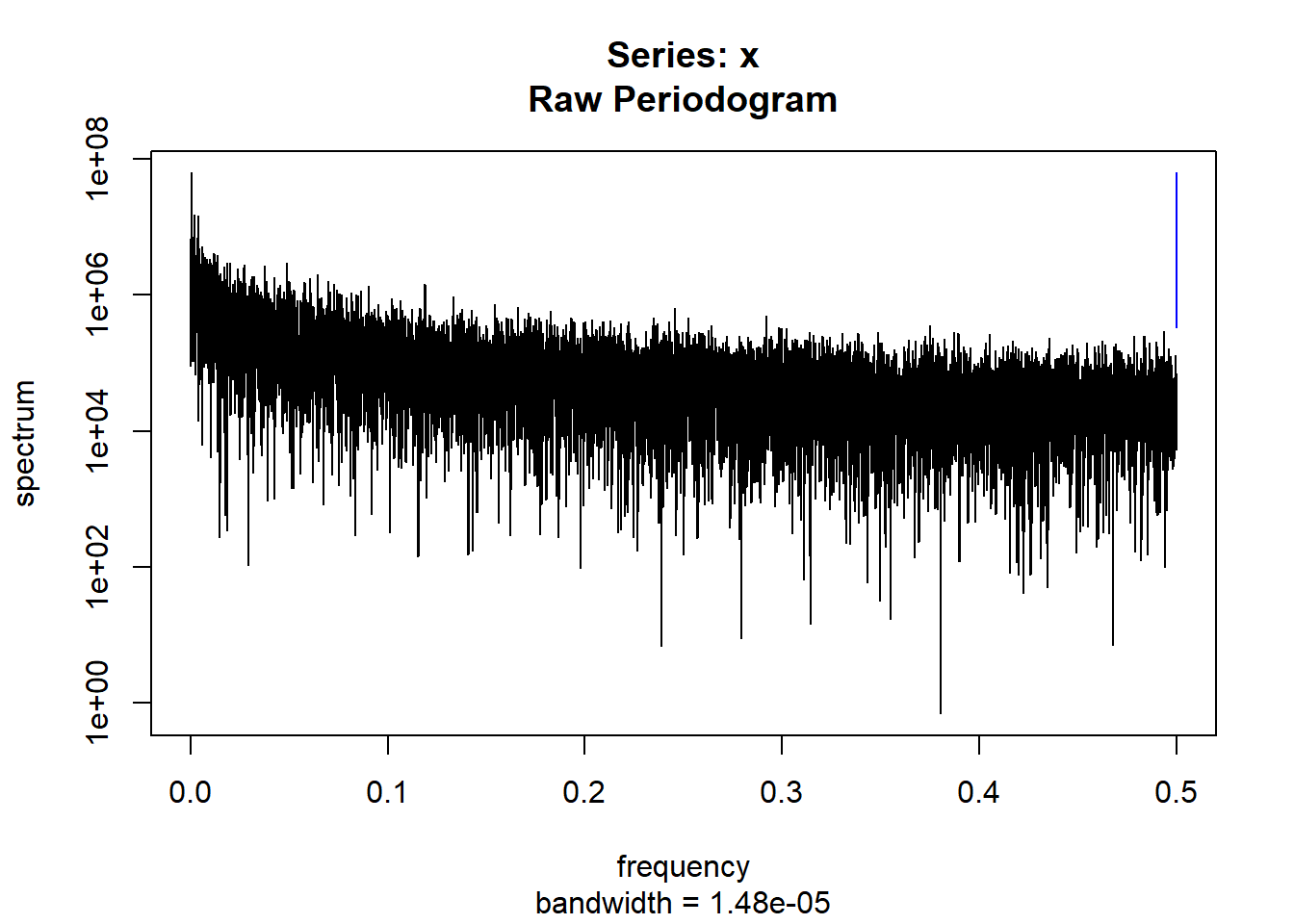
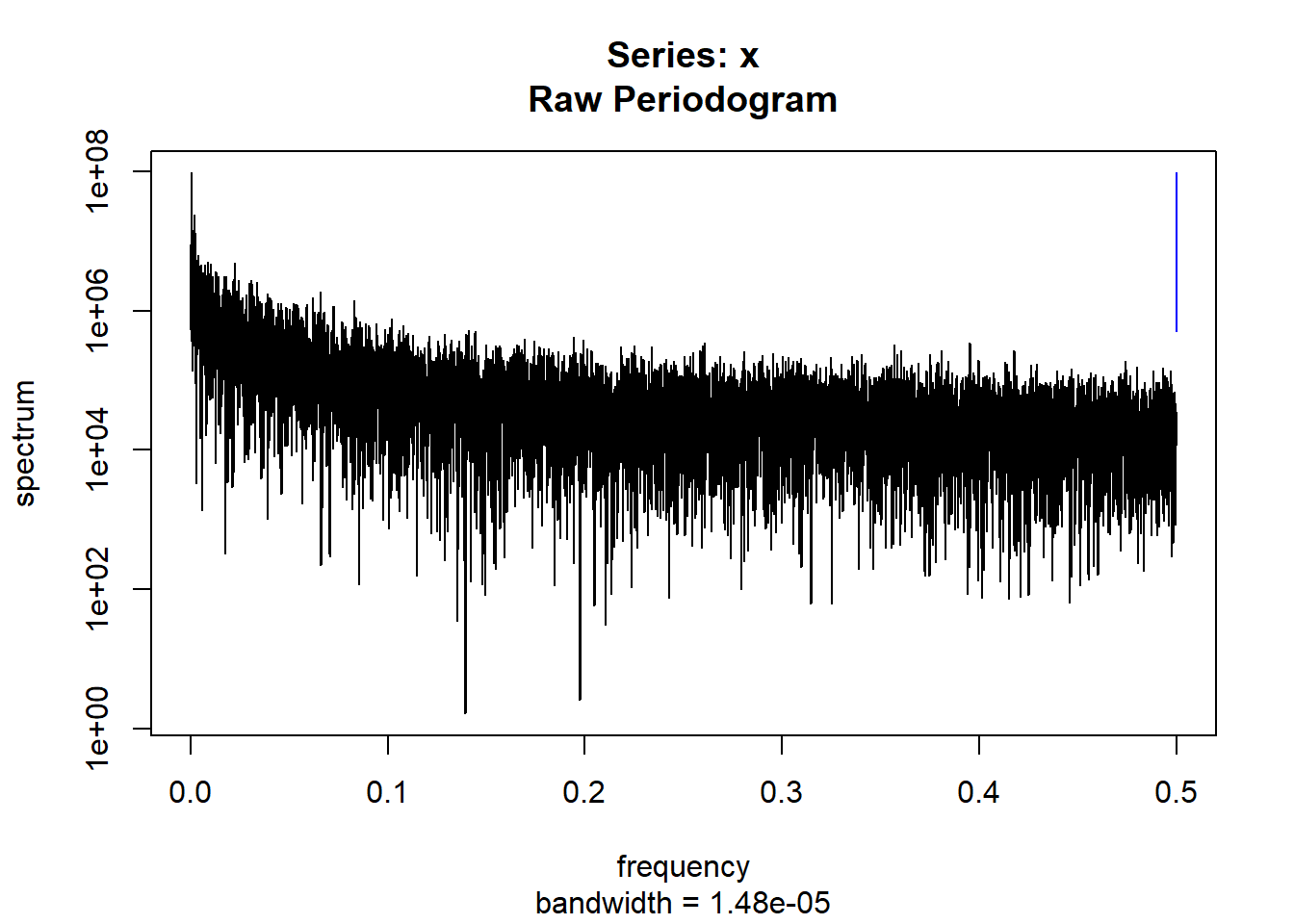
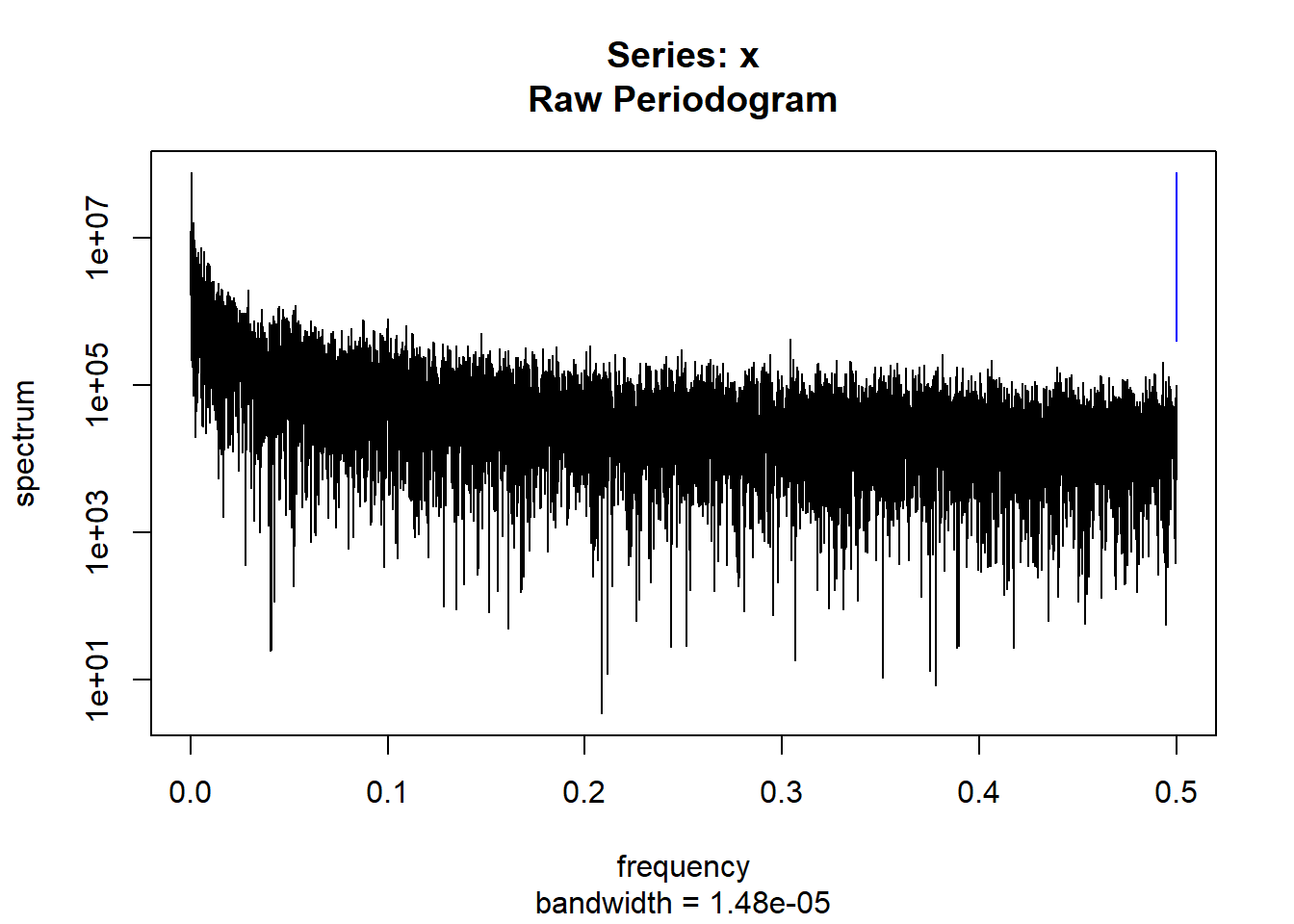
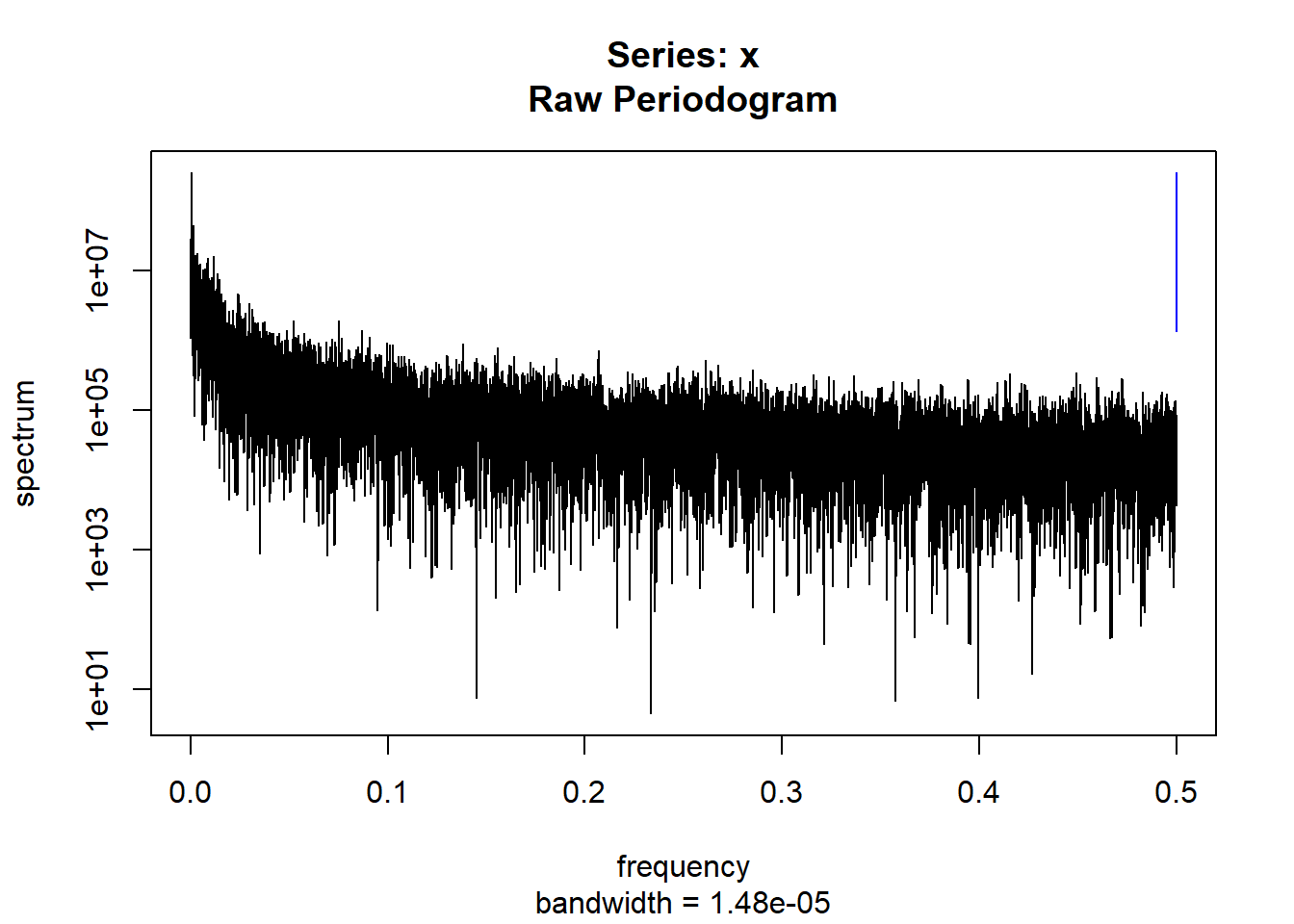
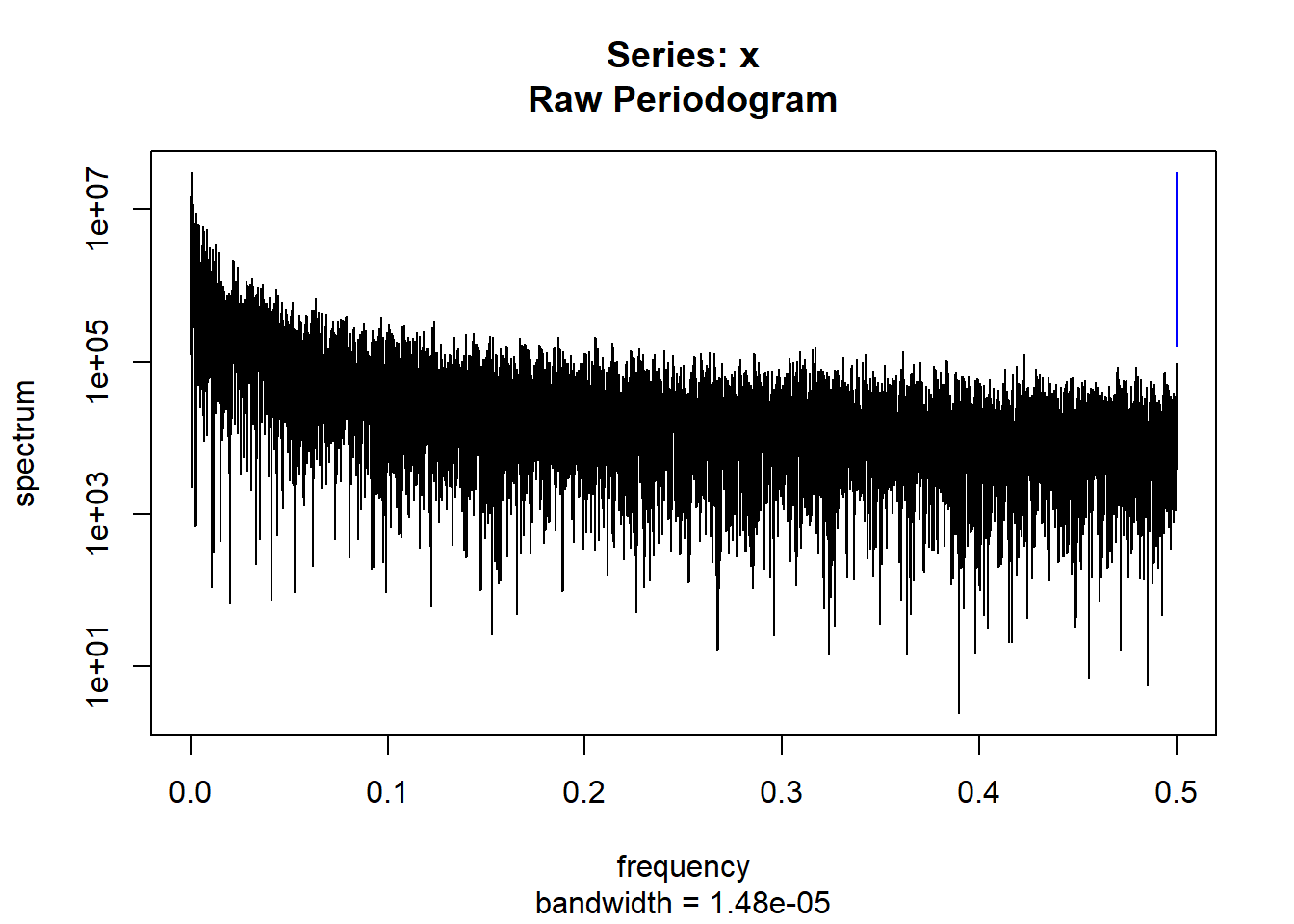
condspectrumlist[[i]]=stats::spectrum(conddatalist[[i]]$activity[1:19299]) #19299 is last minute available for all subjects
condmeanvariabilitystats[[i]]=meanvariabilitystats(conddatalist[[i]]$activity)
conddtvemstage1[[i]]=dtvemstage1(conddatalist[[i]]$activity)
}
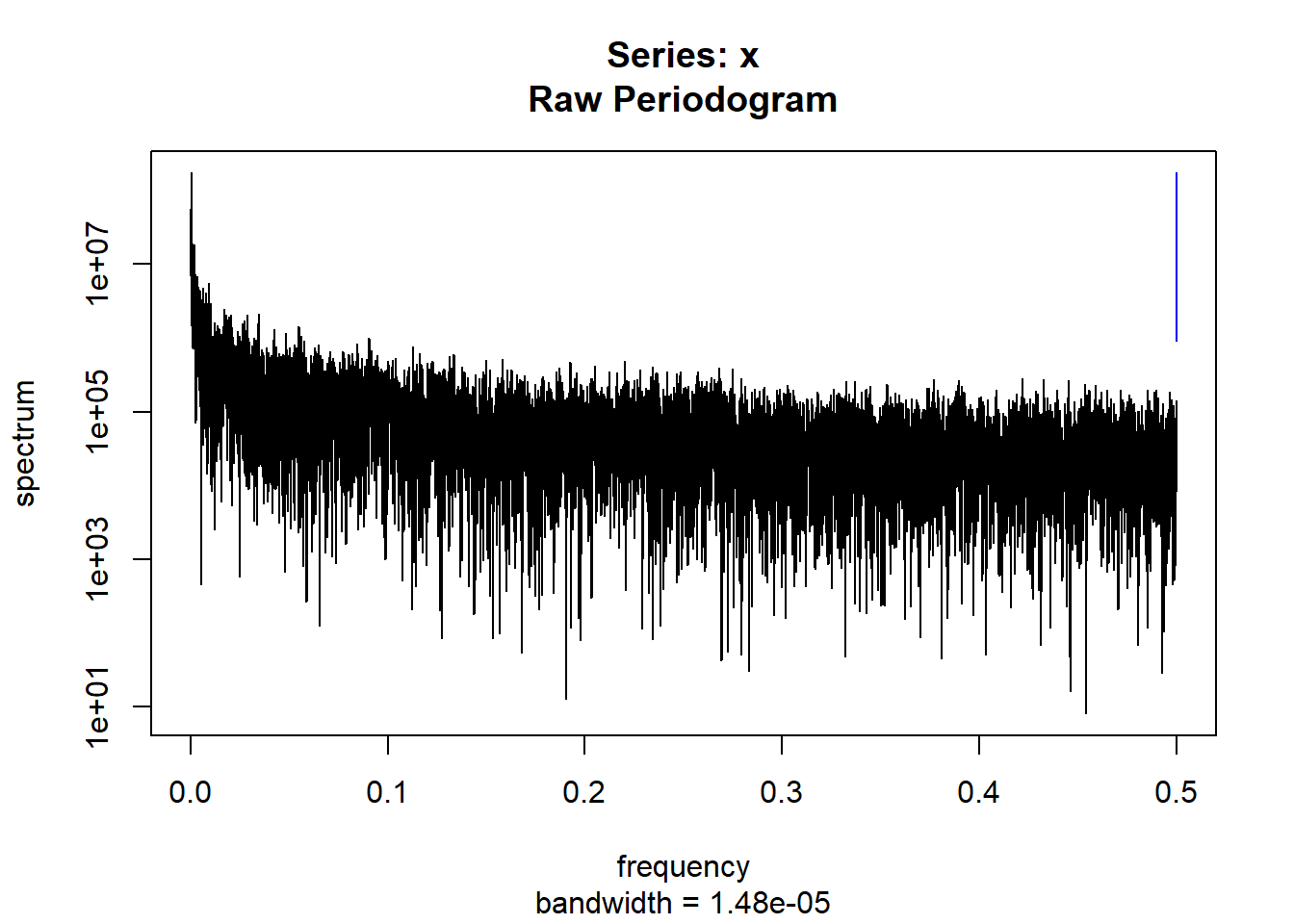
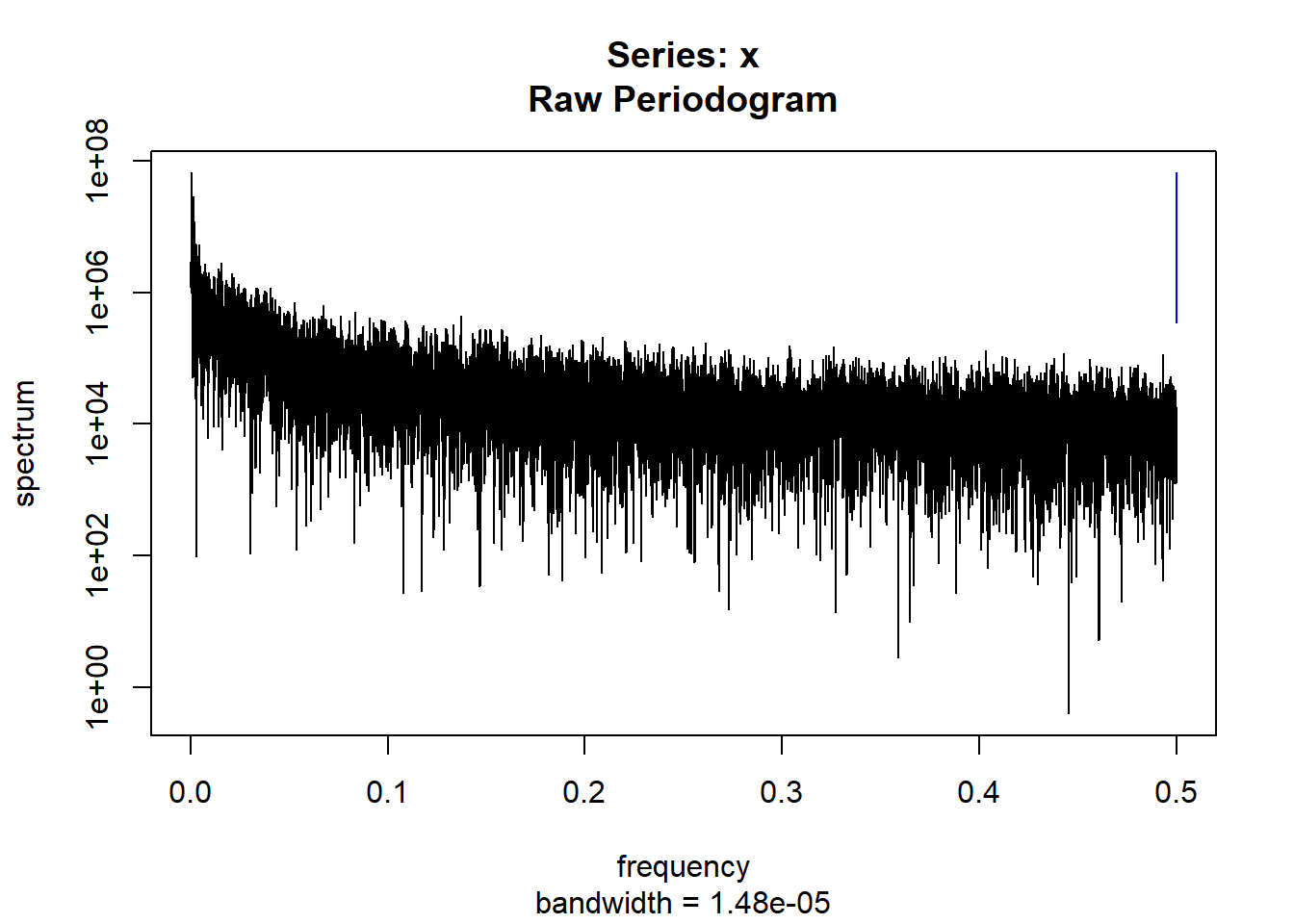
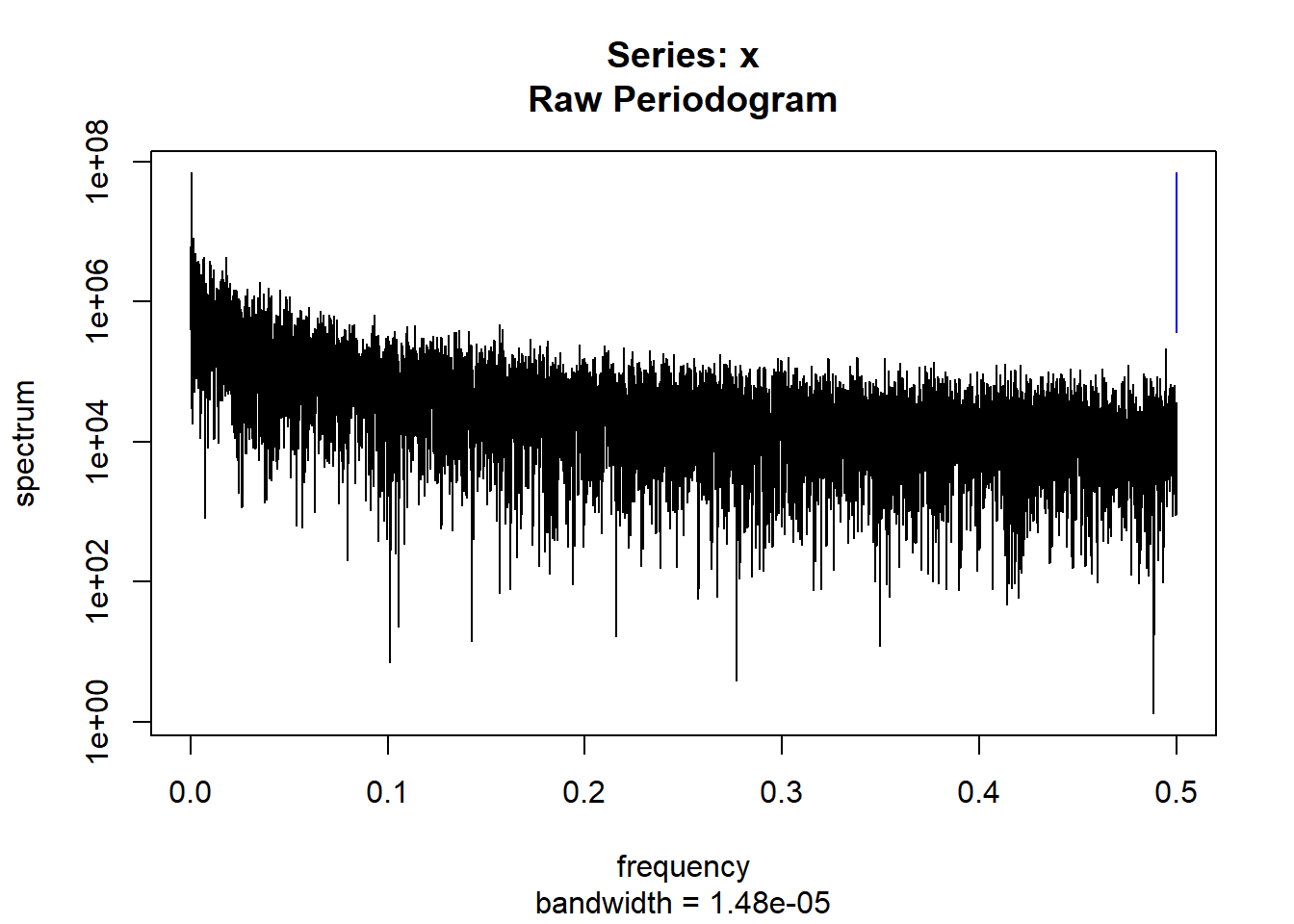
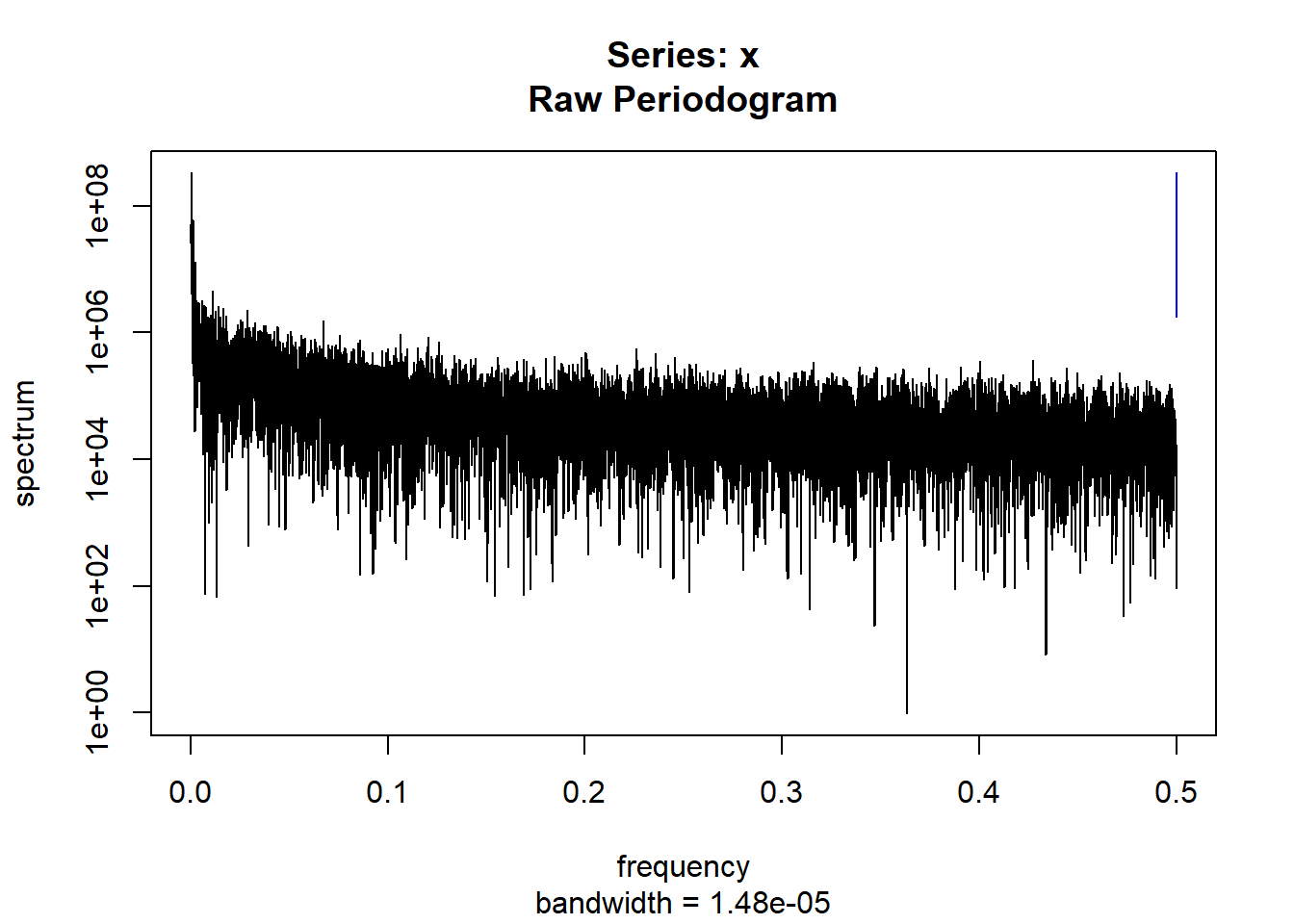
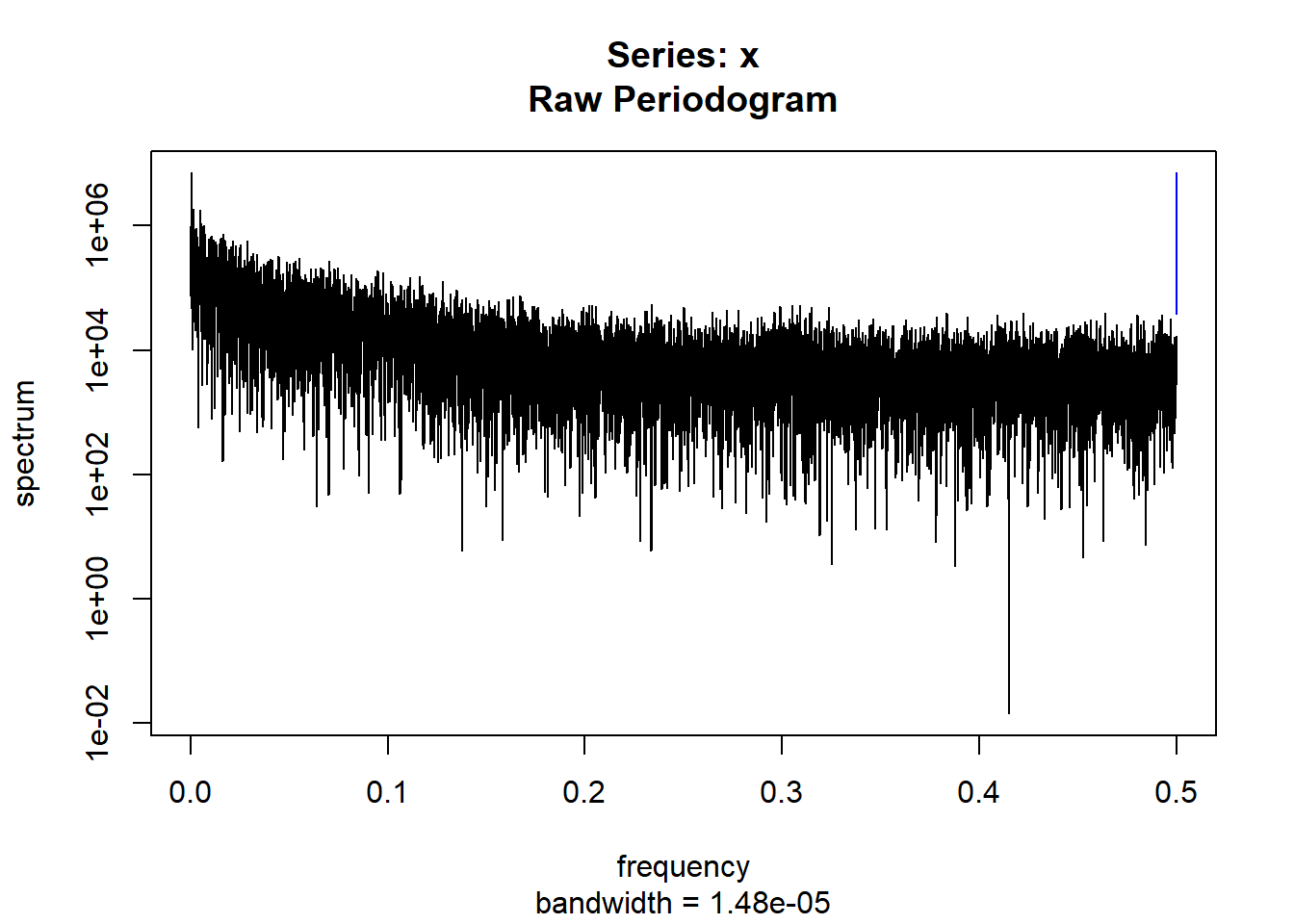
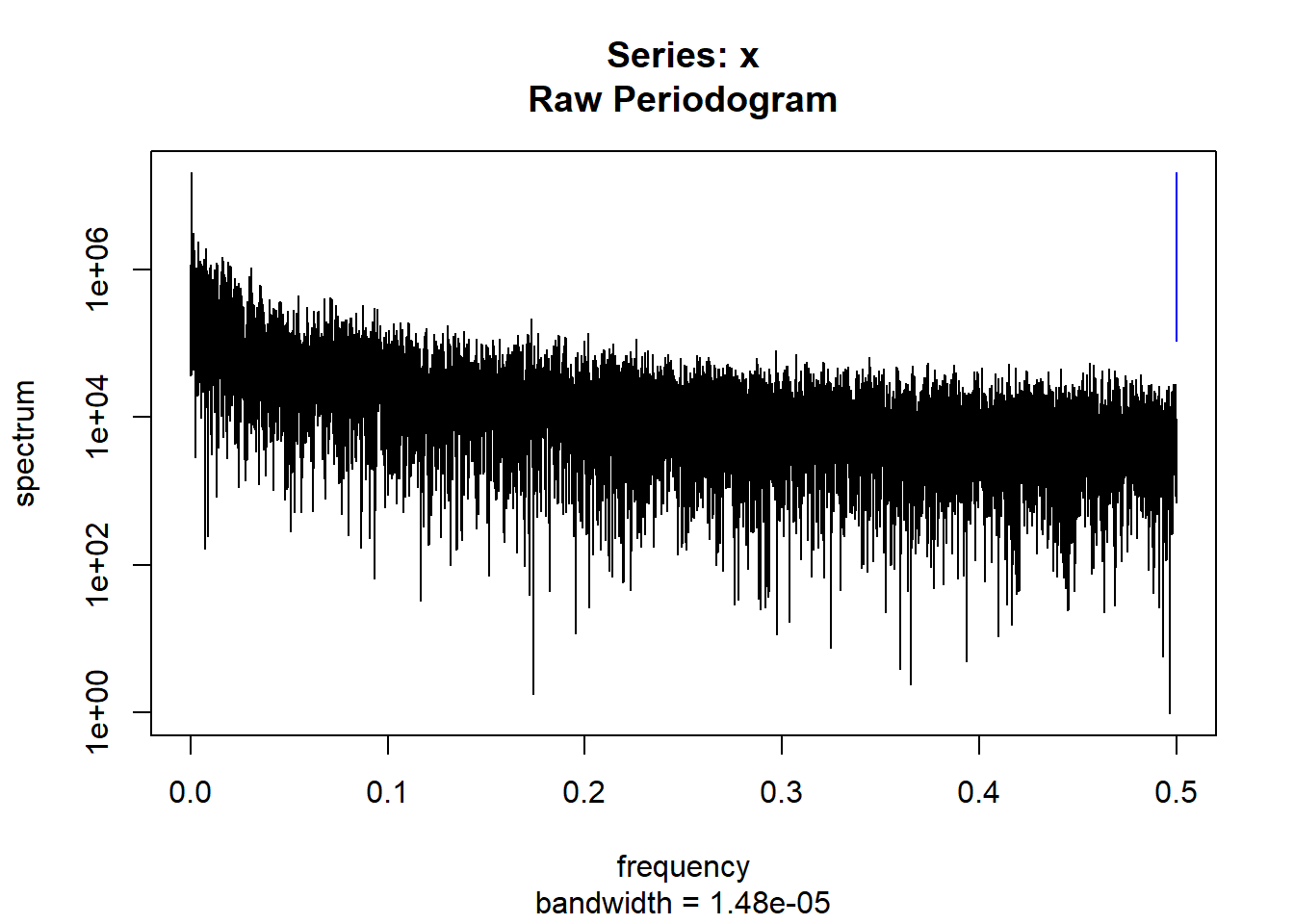
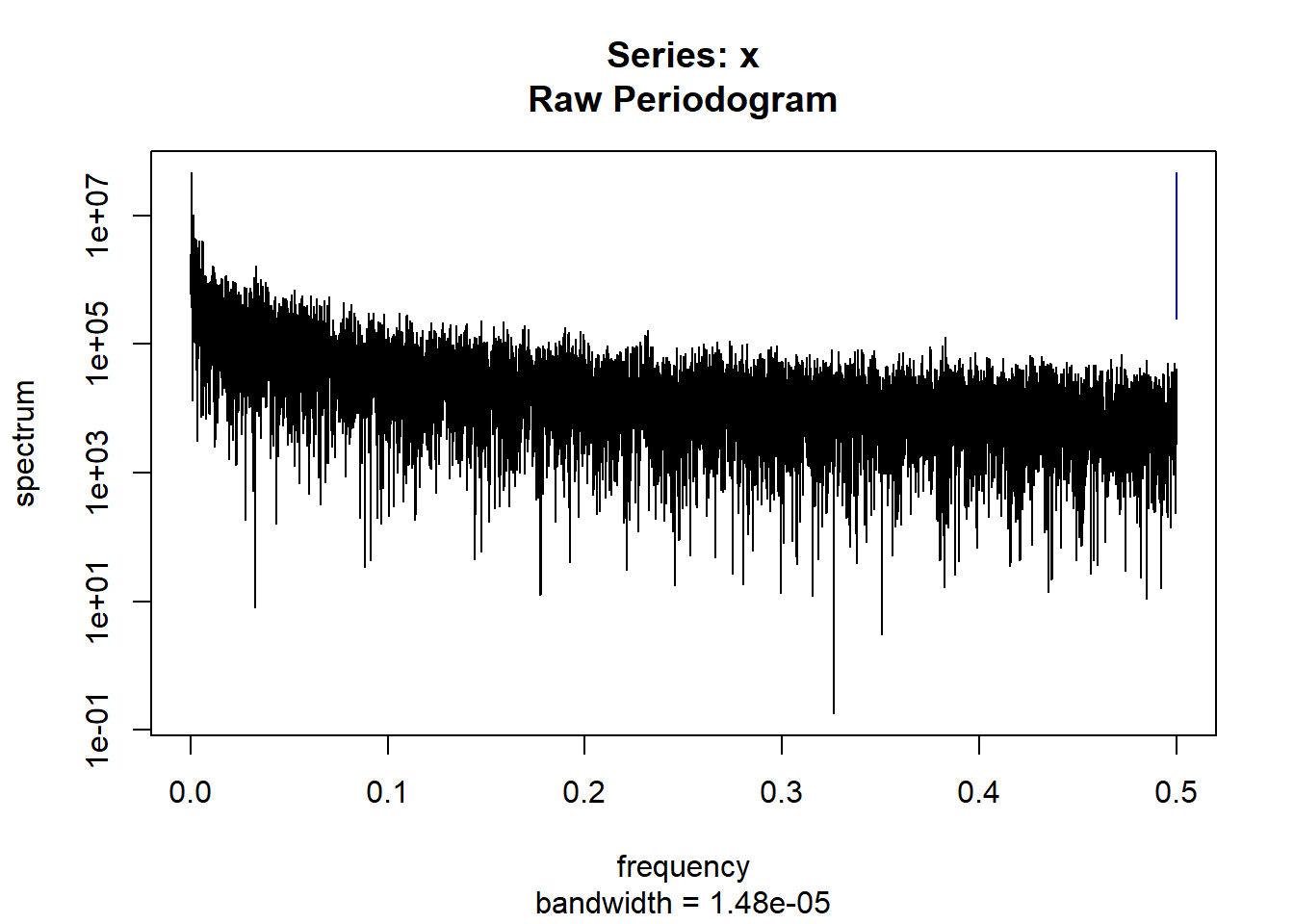
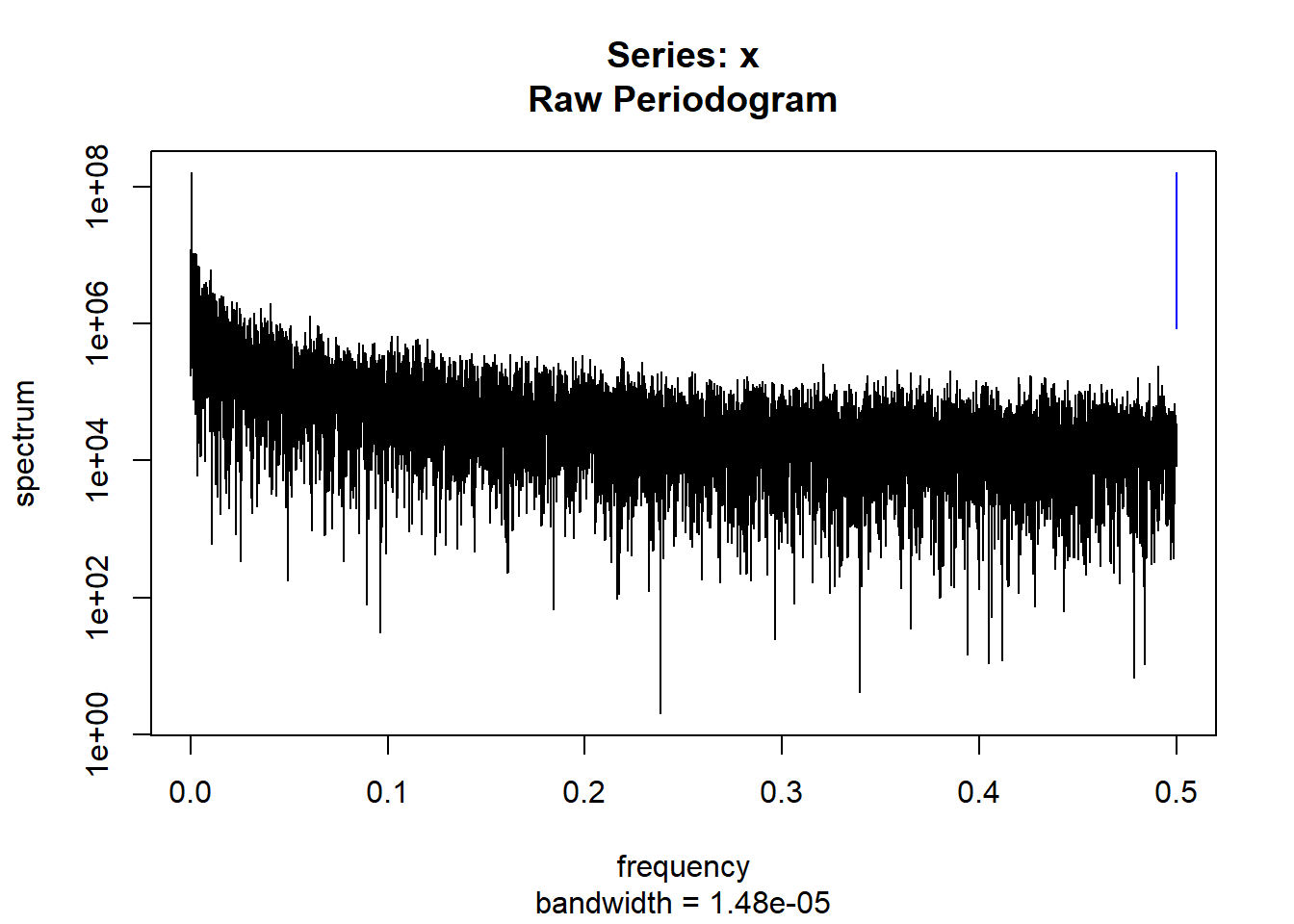
controllist=list.files("control/")
library(gtools)
controllist=mixedsort(controllist) #PUTS THEM IN NUMERICAL ORDER
controldatalist=list()
controlspectrumlist=list()
controlmeanvariabilitystats=list()
controldtvemstage1=list()
for(i in 1:length(controllist)){
controldatalist[[i]]=read.csv(paste("control/",controllist[i],sep=""))
controlspectrumlist[[i]]=stats::spectrum(controldatalist[[i]]$activity[1:19299]) #19299 is last minute available for all subjects
controlmeanvariabilitystats[[i]]=meanvariabilitystats(controldatalist[[i]]$activity)
controldtvemstage1[[i]]=dtvemstage1(controldatalist[[i]]$activity)
}
Next merge the features into the main dataset.
scores[,paste("f",1:9929,sep="")]=NA
#IGNORE SPECTRAL ANALSYSI FOR NOW
for(i in 1:length(condlist)){
scores[i,paste("f",1:109,sep="")]=condmeanvariabilitystats[[i]]
scores[i,paste("f",110:209,sep="")]=conddtvemstage1[[i]]
scores[i,paste("f",210:9929,sep="")]=condspectrumlist[[i]]$spec
}
for(i in 1:length(controllist)){
scores[(i+23),paste("f",1:109,sep="")]=controlmeanvariabilitystats[[i]]
scores[(i+23),paste("f",110:209,sep="")]=controldtvemstage1[[i]]
scores[(i+23),paste("f",210:9929,sep="")]=controlspectrumlist[[i]]$spec
}Result 1: Diagnostic Group Status
Define the outcome.
scores$TYPE=c(rep("Patient",length(condlist)),rep("Control",length(controllist)))Create the training dataset for the mood classification. Note that this is important so that only the biomarker features are use in predicting the diagnostic status.
traindata=scores[,c("TYPE",paste("f",1:9929,sep=""))]Train a machine learning model utilizing xgboost and leave-one-out cross-validation.
train_control<- trainControl(method="LOOCV",savePredictions = TRUE)
set.seed(87626) #SET A RANDOM SEED
model<- train(TYPE~., data=traindata, trControl=train_control, method="xgbTree",na.action=na.pass) #xgboost## Loading required package: xgboost## Loading required package: plyr##
## Attaching package: 'plyr'## The following objects are masked from 'package:Hmisc':
##
## is.discrete, summarizemodel## eXtreme Gradient Boosting
##
## 55 samples
## 9929 predictors
## 2 classes: 'Control', 'Patient'
##
## No pre-processing
## Resampling: Leave-One-Out Cross-Validation
## Summary of sample sizes: 54, 54, 54, 54, 54, 54, ...
## Resampling results across tuning parameters:
##
## nrounds max_depth eta colsample_bytree subsample Accuracy
## 50 1 0.3 0.6 0.50 0.6909091
## 50 1 0.3 0.6 0.75 0.7636364
## 50 1 0.3 0.6 1.00 0.8909091
## 50 1 0.3 0.8 0.50 0.7454545
## 50 1 0.3 0.8 0.75 0.7636364
## 50 1 0.3 0.8 1.00 0.8727273
## 50 1 0.4 0.6 0.50 0.6727273
## 50 1 0.4 0.6 0.75 0.7454545
## 50 1 0.4 0.6 1.00 0.8909091
## 50 1 0.4 0.8 0.50 0.8000000
## 50 1 0.4 0.8 0.75 0.7818182
## 50 1 0.4 0.8 1.00 0.8363636
## 50 2 0.3 0.6 0.50 0.7818182
## 50 2 0.3 0.6 0.75 0.6909091
## 50 2 0.3 0.6 1.00 0.6909091
## 50 2 0.3 0.8 0.50 0.6727273
## 50 2 0.3 0.8 0.75 0.7818182
## 50 2 0.3 0.8 1.00 0.7636364
## 50 2 0.4 0.6 0.50 0.6727273
## 50 2 0.4 0.6 0.75 0.6909091
## 50 2 0.4 0.6 1.00 0.7272727
## 50 2 0.4 0.8 0.50 0.7454545
## 50 2 0.4 0.8 0.75 0.7272727
## 50 2 0.4 0.8 1.00 0.7272727
## 50 3 0.3 0.6 0.50 0.6181818
## 50 3 0.3 0.6 0.75 0.6363636
## 50 3 0.3 0.6 1.00 0.7272727
## 50 3 0.3 0.8 0.50 0.7454545
## 50 3 0.3 0.8 0.75 0.7454545
## 50 3 0.3 0.8 1.00 0.7272727
## 50 3 0.4 0.6 0.50 0.7272727
## 50 3 0.4 0.6 0.75 0.7454545
## 50 3 0.4 0.6 1.00 0.7636364
## 50 3 0.4 0.8 0.50 0.7272727
## 50 3 0.4 0.8 0.75 0.7090909
## 50 3 0.4 0.8 1.00 0.7272727
## 100 1 0.3 0.6 0.50 0.6181818
## 100 1 0.3 0.6 0.75 0.7636364
## 100 1 0.3 0.6 1.00 0.8909091
## 100 1 0.3 0.8 0.50 0.7454545
## 100 1 0.3 0.8 0.75 0.7818182
## 100 1 0.3 0.8 1.00 0.8727273
## 100 1 0.4 0.6 0.50 0.6727273
## 100 1 0.4 0.6 0.75 0.7636364
## 100 1 0.4 0.6 1.00 0.8909091
## 100 1 0.4 0.8 0.50 0.7818182
## 100 1 0.4 0.8 0.75 0.7818182
## 100 1 0.4 0.8 1.00 0.8363636
## 100 2 0.3 0.6 0.50 0.7272727
## 100 2 0.3 0.6 0.75 0.6909091
## 100 2 0.3 0.6 1.00 0.6909091
## 100 2 0.3 0.8 0.50 0.6909091
## 100 2 0.3 0.8 0.75 0.7818182
## 100 2 0.3 0.8 1.00 0.7636364
## 100 2 0.4 0.6 0.50 0.6909091
## 100 2 0.4 0.6 0.75 0.6909091
## 100 2 0.4 0.6 1.00 0.7272727
## 100 2 0.4 0.8 0.50 0.7090909
## 100 2 0.4 0.8 0.75 0.7272727
## 100 2 0.4 0.8 1.00 0.7272727
## 100 3 0.3 0.6 0.50 0.6363636
## 100 3 0.3 0.6 0.75 0.6363636
## 100 3 0.3 0.6 1.00 0.7272727
## 100 3 0.3 0.8 0.50 0.7636364
## 100 3 0.3 0.8 0.75 0.7818182
## 100 3 0.3 0.8 1.00 0.7272727
## 100 3 0.4 0.6 0.50 0.7454545
## 100 3 0.4 0.6 0.75 0.7090909
## 100 3 0.4 0.6 1.00 0.7636364
## 100 3 0.4 0.8 0.50 0.7090909
## 100 3 0.4 0.8 0.75 0.7090909
## 100 3 0.4 0.8 1.00 0.7272727
## 150 1 0.3 0.6 0.50 0.6545455
## 150 1 0.3 0.6 0.75 0.7454545
## 150 1 0.3 0.6 1.00 0.8909091
## 150 1 0.3 0.8 0.50 0.7454545
## 150 1 0.3 0.8 0.75 0.7454545
## 150 1 0.3 0.8 1.00 0.8727273
## 150 1 0.4 0.6 0.50 0.6545455
## 150 1 0.4 0.6 0.75 0.7454545
## 150 1 0.4 0.6 1.00 0.8909091
## 150 1 0.4 0.8 0.50 0.7818182
## 150 1 0.4 0.8 0.75 0.7818182
## 150 1 0.4 0.8 1.00 0.8363636
## 150 2 0.3 0.6 0.50 0.7454545
## 150 2 0.3 0.6 0.75 0.6909091
## 150 2 0.3 0.6 1.00 0.6909091
## 150 2 0.3 0.8 0.50 0.6727273
## 150 2 0.3 0.8 0.75 0.7818182
## 150 2 0.3 0.8 1.00 0.7636364
## 150 2 0.4 0.6 0.50 0.6727273
## 150 2 0.4 0.6 0.75 0.6727273
## 150 2 0.4 0.6 1.00 0.7272727
## 150 2 0.4 0.8 0.50 0.7272727
## 150 2 0.4 0.8 0.75 0.7272727
## 150 2 0.4 0.8 1.00 0.7272727
## 150 3 0.3 0.6 0.50 0.6363636
## 150 3 0.3 0.6 0.75 0.6181818
## 150 3 0.3 0.6 1.00 0.7272727
## 150 3 0.3 0.8 0.50 0.7454545
## 150 3 0.3 0.8 0.75 0.7454545
## 150 3 0.3 0.8 1.00 0.7272727
## 150 3 0.4 0.6 0.50 0.7454545
## 150 3 0.4 0.6 0.75 0.7454545
## 150 3 0.4 0.6 1.00 0.7636364
## 150 3 0.4 0.8 0.50 0.7272727
## 150 3 0.4 0.8 0.75 0.7090909
## 150 3 0.4 0.8 1.00 0.7272727
## Kappa
## 0.3529412
## 0.5112782
## 0.7730399
## 0.4500000
## 0.4989488
## 0.7335640
## 0.3274457
## 0.4704264
## 0.7730399
## 0.5813149
## 0.5285714
## 0.6574394
## 0.5345557
## 0.3364088
## 0.3447793
## 0.3105850
## 0.5460798
## 0.4989488
## 0.3105850
## 0.3529412
## 0.4290657
## 0.4704264
## 0.4069015
## 0.4144784
## 0.2006920
## 0.2434663
## 0.4218641
## 0.4704264
## 0.4704264
## 0.4218641
## 0.4218641
## 0.4569817
## 0.4989488
## 0.4218641
## 0.3871866
## 0.4290657
## 0.1906097
## 0.5112782
## 0.7730399
## 0.4500000
## 0.5345557
## 0.7335640
## 0.3274457
## 0.5112782
## 0.7730399
## 0.5403900
## 0.5285714
## 0.6574394
## 0.4218641
## 0.3364088
## 0.3447793
## 0.3364088
## 0.5460798
## 0.4989488
## 0.3364088
## 0.3529412
## 0.4290657
## 0.4021739
## 0.4069015
## 0.4144784
## 0.2339833
## 0.2434663
## 0.4218641
## 0.5051903
## 0.5403900
## 0.4218641
## 0.4637883
## 0.3794076
## 0.4989488
## 0.3794076
## 0.3871866
## 0.4290657
## 0.2676945
## 0.4704264
## 0.7730399
## 0.4500000
## 0.4500000
## 0.7335640
## 0.2857143
## 0.4704264
## 0.7730399
## 0.5403900
## 0.5285714
## 0.6574394
## 0.4569817
## 0.3364088
## 0.3447793
## 0.3018336
## 0.5460798
## 0.4989488
## 0.3018336
## 0.3191197
## 0.4290657
## 0.4360902
## 0.4069015
## 0.4144784
## 0.2339833
## 0.2006920
## 0.4218641
## 0.4704264
## 0.4637883
## 0.4218641
## 0.4637883
## 0.4500000
## 0.4989488
## 0.4144784
## 0.3871866
## 0.4290657
##
## Tuning parameter 'gamma' was held constant at a value of 0
##
## Tuning parameter 'min_child_weight' was held constant at a value of 1
## Accuracy was used to select the optimal model using the largest value.
## The final values used for the model were nrounds = 50, max_depth = 1,
## eta = 0.3, gamma = 0, colsample_bytree = 0.6, min_child_weight = 1
## and subsample = 1.List the most important biomarkers.
varImp(model)## xgbTree variable importance
##
## Overall
## f385 100.0000
## f6107 98.3969
## f2895 97.6980
## f2194 54.2520
## f6304 47.7481
## f616 38.2510
## f1297 29.4178
## f8410 27.3270
## f8158 25.0654
## f1658 18.8667
## f3759 11.7415
## f9762 8.1432
## f5381 6.0256
## f290 5.1177
## f340 3.3526
## f3091 2.6076
## f5833 0.1289
## f6225 0.0000Next plot the classification results.
ggplotConfusionMatrix <- function(m){
mytitle <- paste("Accuracy", percent_format()(m$overall[1]),
"Kappa", percent_format()(m$overall[2]))
p <-
ggplot(data = as.data.frame(m$table) ,
aes(x = Reference, y = Prediction)) +
geom_tile(aes(fill = log(Freq)), colour = "white") +
scale_fill_gradient(low = "white", high = "steelblue") +
geom_text(aes(x = Reference, y = Prediction, label = Freq)) +
theme(legend.position = "none") +
ggtitle("Diagnostic Status",subtitle=mytitle)
return(p)
}
xgpred=model$pred$pred[model$pred$eta==model$bestTune$eta&model$pred$max_depth==model$bestTune$max_depth&model$pred$gamma==model$bestTune$gamma&model$pred$colsample_bytree==model$bestTune$colsample_bytree&model$pred$min_child_weight==model$bestTune$min_child_weight&model$pred$subsample==model$bestTune$subsample&model$pred$nrounds==model$bestTune$nrounds]
observed=scores$TYPE
ggplotConfusionMatrix(caret::confusionMatrix(xgpred,observed))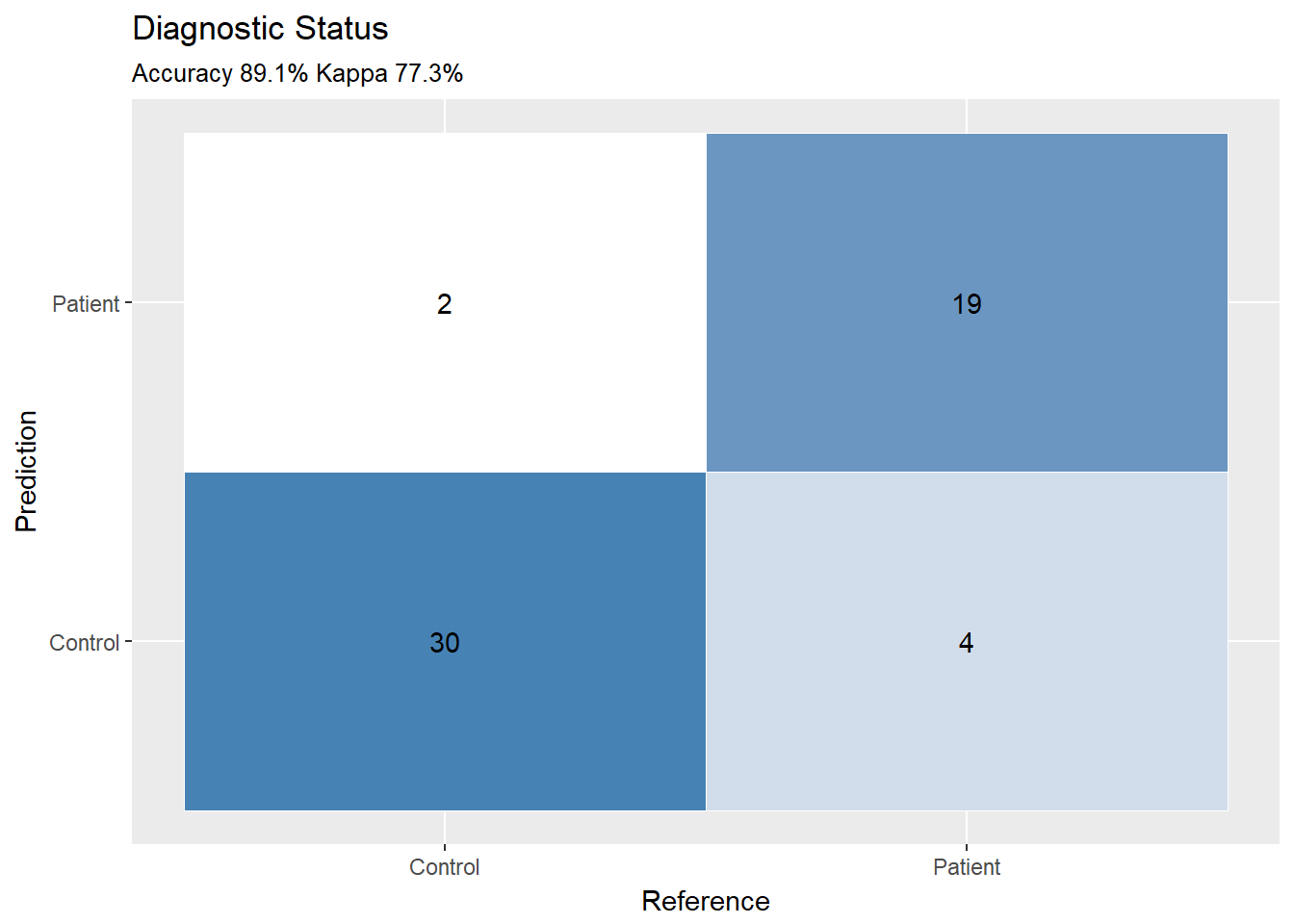
Calculate the diagnostic group’s results.
caret::confusionMatrix(xgpred,observed)## Confusion Matrix and Statistics
##
## Reference
## Prediction Control Patient
## Control 30 4
## Patient 2 19
##
## Accuracy : 0.8909
## 95% CI : (0.7775, 0.9589)
## No Information Rate : 0.5818
## P-Value [Acc > NIR] : 5.513e-07
##
## Kappa : 0.773
## Mcnemar's Test P-Value : 0.6831
##
## Sensitivity : 0.9375
## Specificity : 0.8261
## Pos Pred Value : 0.8824
## Neg Pred Value : 0.9048
## Prevalence : 0.5818
## Detection Rate : 0.5455
## Detection Prevalence : 0.6182
## Balanced Accuracy : 0.8818
##
## 'Positive' Class : Control
## Result 2: Predicting Change in Depression
The next phase is to predict the change in depression across the two weeks.
Define the training set for the symptoms set.
scores$changedep=scores$madrs2-scores$madrs1 #DEFINE CHANGE IN SYMPTOMS
traindataSX=scores[,c("changedep",paste("f",1:9929,sep=""))] #DEFINE TRAINING SET
traindataSX=traindataSX[!is.na(traindataSX$changedep),] #only use the patients.Define a function that will maximize the correlation between variables. Note that the correlation function will result in a negative number so all predictions need to be reversed.
cormax <- function(data, model = NULL,lev=NULL) {
y_pred = data$pred
y_true = data$obs
cormax <- cor(y_pred,y_true)
c(cormaxout=cormax)
}Train the model.
train_control<- trainControl(method="LOOCV",savePredictions = TRUE,summaryFunction = cormax)
set.seed(38552) #min(modelSX$results$cormaxout)=-0.7819468
modelSX<- train(changedep~., data=traindataSX, trControl=train_control, method="xgbTree",na.action=na.pass,maximize=FALSE,metric="cormaxout") #xgboost
modelSX ## eXtreme Gradient Boosting
##
## 23 samples
## 9929 predictors
##
## No pre-processing
## Resampling: Leave-One-Out Cross-Validation
## Summary of sample sizes: 22, 22, 22, 22, 22, 22, ...
## Resampling results across tuning parameters:
##
## nrounds max_depth eta colsample_bytree subsample cormaxout
## 50 1 0.3 0.6 0.50 0.16617190
## 50 1 0.3 0.6 0.75 -0.14486941
## 50 1 0.3 0.6 1.00 -0.67087572
## 50 1 0.3 0.8 0.50 -0.32786366
## 50 1 0.3 0.8 0.75 -0.52801809
## 50 1 0.3 0.8 1.00 -0.78194675
## 50 1 0.4 0.6 0.50 0.04267227
## 50 1 0.4 0.6 0.75 -0.22606989
## 50 1 0.4 0.6 1.00 -0.58630595
## 50 1 0.4 0.8 0.50 -0.47850903
## 50 1 0.4 0.8 0.75 -0.62954059
## 50 1 0.4 0.8 1.00 -0.58639334
## 50 2 0.3 0.6 0.50 -0.41075895
## 50 2 0.3 0.6 0.75 -0.09244586
## 50 2 0.3 0.6 1.00 -0.50194429
## 50 2 0.3 0.8 0.50 -0.14716882
## 50 2 0.3 0.8 0.75 -0.51548546
## 50 2 0.3 0.8 1.00 -0.37542250
## 50 2 0.4 0.6 0.50 -0.45288506
## 50 2 0.4 0.6 0.75 -0.33770685
## 50 2 0.4 0.6 1.00 -0.54328952
## 50 2 0.4 0.8 0.50 -0.41916662
## 50 2 0.4 0.8 0.75 -0.23226072
## 50 2 0.4 0.8 1.00 -0.30689632
## 50 3 0.3 0.6 0.50 -0.38902617
## 50 3 0.3 0.6 0.75 0.21024049
## 50 3 0.3 0.6 1.00 -0.31715668
## 50 3 0.3 0.8 0.50 -0.18758863
## 50 3 0.3 0.8 0.75 -0.49439659
## 50 3 0.3 0.8 1.00 -0.46324068
## 50 3 0.4 0.6 0.50 -0.12577266
## 50 3 0.4 0.6 0.75 -0.43003281
## 50 3 0.4 0.6 1.00 -0.49639161
## 50 3 0.4 0.8 0.50 -0.13755568
## 50 3 0.4 0.8 0.75 0.07731012
## 50 3 0.4 0.8 1.00 -0.30194459
## 100 1 0.3 0.6 0.50 0.15176723
## 100 1 0.3 0.6 0.75 -0.14680596
## 100 1 0.3 0.6 1.00 -0.67157327
## 100 1 0.3 0.8 0.50 -0.33786952
## 100 1 0.3 0.8 0.75 -0.52507854
## 100 1 0.3 0.8 1.00 -0.78012772
## 100 1 0.4 0.6 0.50 0.05249711
## 100 1 0.4 0.6 0.75 -0.22685517
## 100 1 0.4 0.6 1.00 -0.58622481
## 100 1 0.4 0.8 0.50 -0.46845677
## 100 1 0.4 0.8 0.75 -0.62825228
## 100 1 0.4 0.8 1.00 -0.58626054
## 100 2 0.3 0.6 0.50 -0.42143889
## 100 2 0.3 0.6 0.75 -0.09244758
## 100 2 0.3 0.6 1.00 -0.50198402
## 100 2 0.3 0.8 0.50 -0.13967037
## 100 2 0.3 0.8 0.75 -0.51493330
## 100 2 0.3 0.8 1.00 -0.37548410
## 100 2 0.4 0.6 0.50 -0.46470840
## 100 2 0.4 0.6 0.75 -0.33792991
## 100 2 0.4 0.6 1.00 -0.54328939
## 100 2 0.4 0.8 0.50 -0.41617313
## 100 2 0.4 0.8 0.75 -0.23227399
## 100 2 0.4 0.8 1.00 -0.30689632
## 100 3 0.3 0.6 0.50 -0.39768087
## 100 3 0.3 0.6 0.75 0.20885109
## 100 3 0.3 0.6 1.00 -0.31719193
## 100 3 0.3 0.8 0.50 -0.18730556
## 100 3 0.3 0.8 0.75 -0.49406211
## 100 3 0.3 0.8 1.00 -0.46322477
## 100 3 0.4 0.6 0.50 -0.12970602
## 100 3 0.4 0.6 0.75 -0.43006568
## 100 3 0.4 0.6 1.00 -0.49639165
## 100 3 0.4 0.8 0.50 -0.13882637
## 100 3 0.4 0.8 0.75 0.07727875
## 100 3 0.4 0.8 1.00 -0.30194464
## 150 1 0.3 0.6 0.50 0.15306324
## 150 1 0.3 0.6 0.75 -0.14665606
## 150 1 0.3 0.6 1.00 -0.67156424
## 150 1 0.3 0.8 0.50 -0.33509150
## 150 1 0.3 0.8 0.75 -0.52505063
## 150 1 0.3 0.8 1.00 -0.78013294
## 150 1 0.4 0.6 0.50 0.05244080
## 150 1 0.4 0.6 0.75 -0.22684606
## 150 1 0.4 0.6 1.00 -0.58622480
## 150 1 0.4 0.8 0.50 -0.46818627
## 150 1 0.4 0.8 0.75 -0.62824085
## 150 1 0.4 0.8 1.00 -0.58626053
## 150 2 0.3 0.6 0.50 -0.42160780
## 150 2 0.3 0.6 0.75 -0.09245073
## 150 2 0.3 0.6 1.00 -0.50198409
## 150 2 0.3 0.8 0.50 -0.13952336
## 150 2 0.3 0.8 0.75 -0.51493350
## 150 2 0.3 0.8 1.00 -0.37548411
## 150 2 0.4 0.6 0.50 -0.46480550
## 150 2 0.4 0.6 0.75 -0.33792367
## 150 2 0.4 0.6 1.00 -0.54328939
## 150 2 0.4 0.8 0.50 -0.41624653
## 150 2 0.4 0.8 0.75 -0.23227661
## 150 2 0.4 0.8 1.00 -0.30689632
## 150 3 0.3 0.6 0.50 -0.39795293
## 150 3 0.3 0.6 0.75 0.20884824
## 150 3 0.3 0.6 1.00 -0.31719194
## 150 3 0.3 0.8 0.50 -0.18778564
## 150 3 0.3 0.8 0.75 -0.49405535
## 150 3 0.3 0.8 1.00 -0.46322477
## 150 3 0.4 0.6 0.50 -0.12968043
## 150 3 0.4 0.6 0.75 -0.43006488
## 150 3 0.4 0.6 1.00 -0.49639165
## 150 3 0.4 0.8 0.50 -0.13872841
## 150 3 0.4 0.8 0.75 0.07727625
## 150 3 0.4 0.8 1.00 -0.30194464
##
## Tuning parameter 'gamma' was held constant at a value of 0
##
## Tuning parameter 'min_child_weight' was held constant at a value of 1
## cormaxout was used to select the optimal model using the smallest value.
## The final values used for the model were nrounds = 50, max_depth = 1,
## eta = 0.3, gamma = 0, colsample_bytree = 0.8, min_child_weight = 1
## and subsample = 1.Identify the predictions vs the observed values.
ps=modelSX$pred[modelSX$pred$eta==modelSX$bestTune$eta&modelSX$pred$max_depth==modelSX$bestTune$max_depth&modelSX$pred$gamma==modelSX$bestTune$gamma&modelSX$pred$colsample_bytree==modelSX$bestTune$colsample_bytree&modelSX$pred$min_child_weight==modelSX$bestTune$min_child_weight&modelSX$pred$subsample==modelSX$bestTune$subsample&modelSX$pred$nrounds==modelSX$bestTune$nrounds,c("pred","obs")]
ps[,1]=ps[,1]*-1 #REVERSE THE PREDICTIONSGet the correlation between the predicted and observed symptom change.
cormat=rcorr(data.matrix(ps))
cormat$r[1,2] #CORRELATION## [1] 0.7819468cormat$P[1,2] #P-VALUE## [1] 1.048242e-05Plot the results.
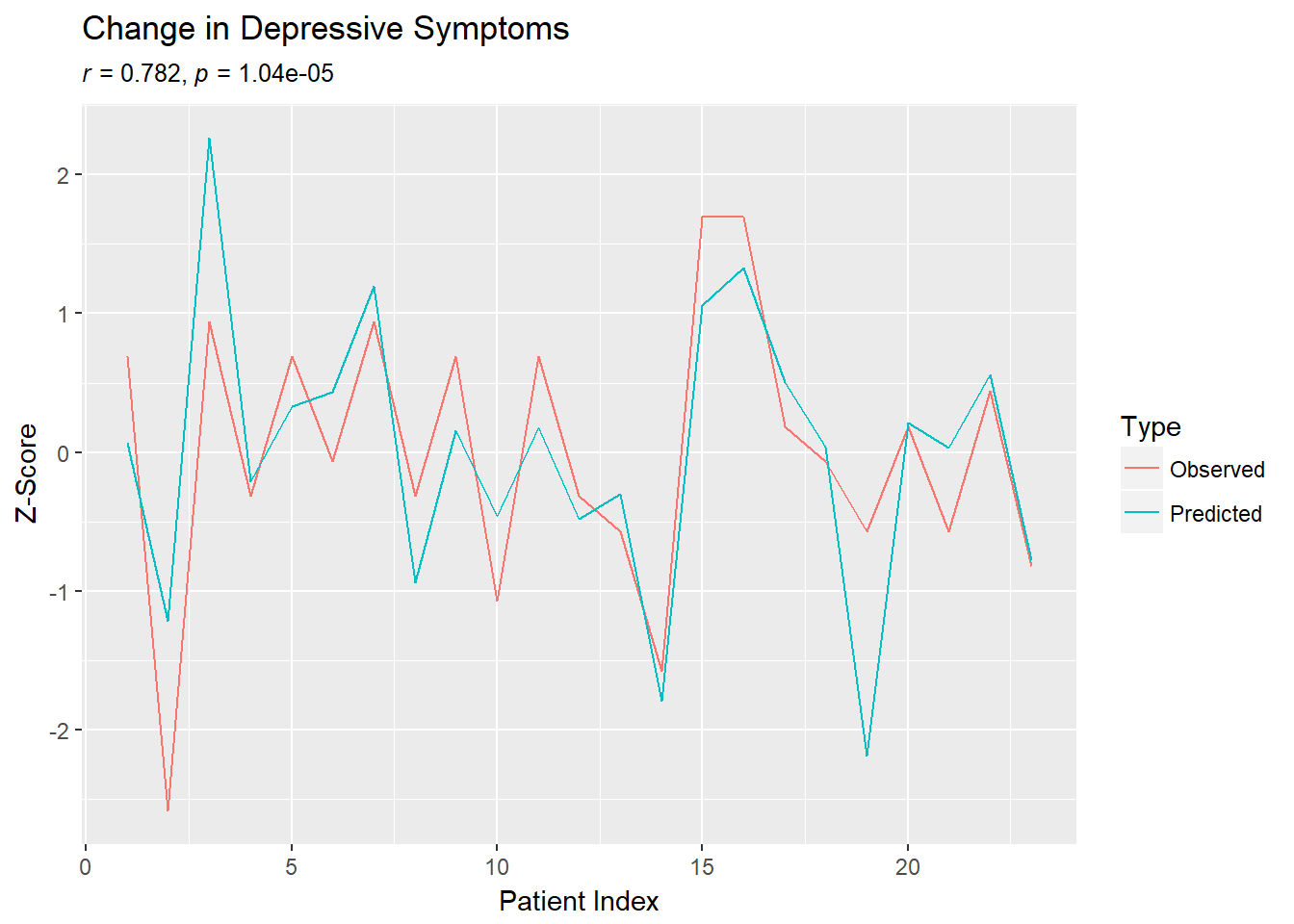
longpreds=data.frame(Type=c(rep("Predicted",23),rep("Observed",23)),PatientIndex=c(1:23,1:23),zscore=c(scale(ps[,1]),scale(ps[,2])))
ggplot(data=longpreds,aes(x=PatientIndex, y=zscore, colour=Type)) +geom_line()+ylab("Z-Score")+xlab("Patient Index")+ggtitle(paste("Change in Depressive Symptoms"),subtitle=expression(paste(italic("r")," = 0.782, ",italic("p")," = 1.04e-05",sep="")))